Immagine e nucleo di una trasformazione

Teorema K.1

1. L'insieme Im(L) è un sottospazio vettoriale di W.

2. Fissate le basi in V e W, sia A una matrice di tipo (m,n) che rappresenta L. Allora

   dim Im(L) = rango di A

Dim. La proprietà 1) segue dalla linearità di L, se y₁=L(x₁) e y₂=L(x₂) e α e β in 𝕂:

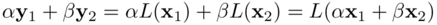
Per dimostrare la 2) osesrviamo che dalla dimostrazione del teorema di rappreesntazione, si vede che Im(L) è generato dai vettori L(u₁), ..., L(u_n). Le colonne della matrice A sono le componenti scalari degli L(u_i) rispetto alla base v₁, ..., v_n di W. Se r tra queste colonne sono indipendenti i corrispondendit vettori L(u_i) sono indipendenti e viceversa. Da ciò segue che r = dim Im(L).

Def. K1 (Nucleo di una trasformazione)- Siano V, W due spazi vettoriali su 𝕂, e sia L: V → W, un'applicazione lineare. Il nucleo dell'applicazione che si indica col simbolo Ker(L), è l'insieme dei vettori di v ∈ V che hanno come immagine il vettore nullo di W, L(v)=0. Ossia l'insieme:

Teorema. K2 Sia L: V → W una trasformazione lineare, il cui Ker = {0}. Se v₁, ..., v_n sono vettori linearmente indipendenti di V allora L(v₁), ..., L(v_n) sono vettori linearmente indipendenti di W.

Dim. Siano x₁, x₂ , ..., x_n coefficienti tali che:

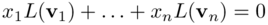
Per linearità si ottiene:

Siccome v₁, ..., v_n sono linearmente indipendenti ciò implica che x_i=0 per i= 1,..,n. Il teorema è così dimostrato. □

Teorema. K3 Sia V uno spazio vettoriale di dimensione n e sia L: V → W una trasformazione lineare, nello spazio W. Vale la seguente identità

Dim. Poniamo k= dim Ker(L) e n = dim V. Scegliamo una base w₁, w₂, ..., w_k del nucleo. Si aggiungono a questa base n -k vettori linearmente indipendenti w₁, w₂, ..., w_n in modo che:

w₁, w₂, ..., w_k, u_k+1,..., u_n

formino una base per V. Sia v un generico vettore di V si può quindi scrivere:

Essendo L(w_j)= 0 per ogni j =1, 2, ...,n, si ha:

per cui L(u_k+1),..., L(u_n) risulta un sistema di generatori per Im(L). Si ha quindi dim Im(L) ≤ n-k.

Facciamo vedere che dim Im(L) = n-k, infatti l'insieme di vettori vettori u_k+1,..., u_n è un insieme linearmente indipendente. Se fossero dipendenti si avrebbe

con qualche β_j diverso da zero. Ciò implicherebbe che il vettore non nullo β_k+1u_k+1 +...+ β_nu_n ∈ Ker(L); ma allora questo vettore si potrebbe scrivere come combinazione lineare dei vettori w_i il che è un assurdo poichè i vettori w_i e u_i sono tra loro linearmente indipendenti.□