Rappresentazione lineare delle trasformazioni lineari

Abbiamo visto che la matrice A_α di ordine 2 realizza una rotazione del piano (attorno all'origine) di un angolo α, nel senso che, preso il vettore (x,y), il vettore trasformato, si ottiene ruotando di un angolo α attorno all'origine (nel senso positivo). In generale, una matrice quadrata A, qudrata di ordine n, traforma un vettore di ℝⁿ in un altro vettore di ℝⁿ mediante il prodotto righe per colonne (pensanso sempre ai vettori come colonne): x ∈ ℝⁿ è trasformato nel vettore Ax ∈ ℝⁿ, nel vettore Ax ∈ ℝ^m.

Infine, considerazioni analoghe valgono per il campo complesso ℂ: una matrice di tipo (m,n) a elementi complessi realizza una trasformazione lineare di ℂⁿ in ℂ^m. Il prossimo teorema afferma che tutte le trasformazioni lineari tra due spazi vetoriali qualsiasi di dimensione finita si possono rappresentare a questo modo.

Teorema 6.1 - Teorema di Rappresentazione - Sia data una applicazione lineare L : V → W con V e W due spazi vettoriali, sul campo 𝕂. Fissate due basi u₁, u₂ , ..., u_n in V e v₁, v₂ , ..., v_m in W, esiste una matrice unica A (m x n) a elementi in 𝕂 che rappresenta L. Nel senso che se, x = x₁ u₁ + x₂ u₂ + ... + x_mu_m, la trasformazione L(x) = y₁ v₁+ y₂ v + ...+ v_m, si può rappresentare in forma matriciale come

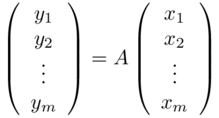
Dim. - I vettori L( u_j ) ∈ W, si poosono esprimere come combinazione lineari dei vettori della base:

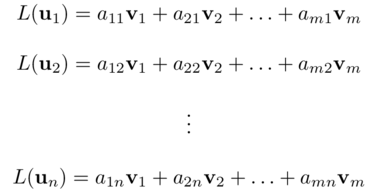
per opportuni coefficienti a_ij ∈ ℝ.

Poniano:

e x = x₁ u₁ + x₂ u₂ + ... + x_mu_m. Si ha per la linearità di L e per le equazioni precedenti:

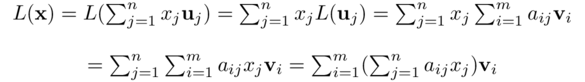
Risulta evidente che le componenti scalari di L(x), rispetto alla base v₁, v₂ , ..., v_m sono date dalla relazione:

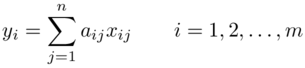
o in forma matriciale

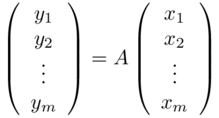
La matrice A è unica nel rappresentare L poichè ogni vettore L( u_j ) si può esprimere in un unico modo come combinazione lineare dei vettori v₁, v₂ , ..., v_m.□

Osservazioni

1. Il teorema di rappresentazione chiarisce il motivo per cui il prodotto di matrici è stato definito proprio in quel modo ("righe per colonne").