Change of Basis

A basis that is suitable for one problem may not be suitable for another, so it is common process in the study of vector spaces to change from one basis to another. Because a basis is the vector space generalization of a coordinate system, changing bases is akin to changing coordinate axes in ℝ² or ℝ³. In this section we will study problems related to change of basis.

Sia V uno spazio vettoriale di dimensione n sul campo 𝕂 e sia L : V → V una funzione lineare. Studiando il teorema di rappresentazione abbiamo visto come, fissando una base di V, sia possibile associare a L una matrice quadrata di ordine n, a coefficienti in 𝕂. Naturalmente, a basi diverse di V corrispondono matrici diverse di L, tutte simili tra loro. Ci si può dunque chiedere se sia possibile trovare una base di V in modo tale che la corrispondente matrice di L assuma una qualche forma canonica (particolarmente semplice) prefissata. Supponiamo, ad esempio, che esista una base di V costituita da vettori v₁, v₂,..., v_n tali che L (v_i) = λ_i v_i , per i = 1, . . . , n, per opportuni scalari λ_i ∈ 𝕂. Rispetto a tale base la matrice di L assumerebbe la seguente forma diagonale

ciò significa che la trasformazione y = L(x) rispetto a questa base si scrive così:

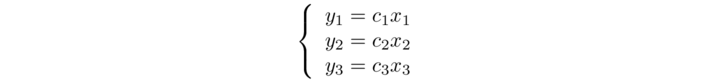
Si tratta di un'espresssione semplice in cui ogni variabile y_i dipende solo dalla variabile x_i anzichè da tutte e tre. Geometricamente significa che abbiamo scelto un opportuno sistema di riferimento in ℝ³ (non necessariamente ortogonale), rispetto al quale la trasformazione agisce come una dilatazione di un certo coefficiente c_i su ciascun asse. Rispetto a questa base i calcoli risultano più semplici e le proprietà della trasformazione appaiono in modo più trasparente. Diremo in questo caso che la trasformazione ha forma diagonale. Vediamo come cambia la rappresentazione di L cambiando la base in ℝⁿ.

If v is a vector in a finite-dimensional vector space V, and if we change the basis for V from a basis B to a basis B', how are the coordinate vectors [v]_B and [v]_B' related? For simplicity, we will solve this problem for two-dimensional spaces.

Let B = {u₁, u₂} and B' = {u₁ , u₂ } be the old and new bases, respectively. We will need the coordinate vectors for the new basis vectors relative to the old basis. Suppose they are

[u₁']_B = (a,b)
[u₂']_B = (c,d)

That is,

[u₁'] = a u₁+ b u₂
[u₂'] = c u₁+ d u₂

Now let v be any vector in V, and let

[v]_B' = (k₁,k₂)

be the new coordinate vector, so that

v = k₁u'₁ + k₂ u'2

In order to find the old coordinates of v, we must express v in terms of the old basis B . To do this, we substitute (4) into (6). This yields

v = k₁ (a u₁ + b u₂ ) + k₂ (c u₁ + d u₂)

Thus, the old coordinate vector for v is

[v]_B = (k₁ a + k₂ c, k₁ b + k₂ d)

che può essere scritta in forma matriciale come

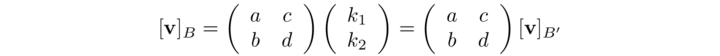
La matrice che compare nella precedente è ottenuta accostando i vettori colonna B' = {u₁ , u₂ } nella vecchia base ed è nota come matrice di passaggio e la indichiamo con S. Se quindi un vettore ha rispetto alla vecchia base coordinate x = (x₁,x₂, x_n) nella nuova base avrà coordinate x̄

x̄ = S^-1 x

Poichè i vettori che costiuiscono la base di B' sono indipendenti det S ≠ 0.

Allora se y = Ax nella base B, nella nuova base B' risulta

ȳ= S^-1 y = S^-1 A x = S^-1 A S x̄

perciò la trasformazione nella nuova base è rappresentata dalla matrice

A' = S^-1AS

Quanto detto inoltre può essere ripetuto per matrici ad elementi complessi, viste come trasformazioni di ℂⁿ in sè.

In questo caso esiste una base 𝕂ⁿ in cui la trasformazione che rispetto alla base B si rappresentava con la matrice A, si rappresenta invece con una matrice diagonale in B'. Il problema che ci poniamo è quindi: data una matrice, decedere se essa è diagonalizzabile, e in caso affermativo determinare la matrice diagonale e la matrice di passaggio. Questo problema è legato ad un altro che ora introdurremo, quello della ricerva di autovalori e autovettori della matrice.

«Thermodynamic Systems Index Autovalori ed Autovettori »