Autovalori ed Autovettori
Definizione 1 - Sia T: V → V un endomorfismo di uno spazio vettoriale V rappresentato dalla matrice A. Un vettore v ≠ 0 di V è un autovettore di T relativo all'autovalore λ se si ha
Av = λ v (1.0)
L'insieme degli autovalori di T cioè degli scalari λ ∈ 𝕂. per cui esista un vettore non nullo v0, soddisfacente la (1.0) - si dice spettro di T, ed è indicato con sp(T). Se λ ∈ sp(T), l'insieme
Vλ = { v ∈ V | T(v) = λv}
è detto autospazio di T relativo all'autovalore λ, ed è un sottospazio di V. Ovviamente λ è un autovalore se e solo se Vλ ≠ {∅}.
In altre parole si stiamo chiedendo se esistono particolari vettori sui quali la trasformazione T agisce come se fosse di tipo diagonale.
In tal caso, preso un qualsiasi vettore tv parallelo v (t ∈ 𝕂) si avrà anche, per linearità:
A(tv) = tAv = (t λ)v
e quindi in questo caso possiamo affermare che la direzione di 𝕂n individuata dal vettore v è trasformata in se stessa.
Scivendo In v al posto di v possiamo riscrivere l'equazione (1.0) come
(A - λIn) v = 0
In questa equazione il vettore v come lo scalare λ è incognito: le componenti del vettore soddisfano perciò un sistema lineare omogeneo n x n. Sappiamo che, perchè esistano vettori v (non nulli) che rislvono la (1.0), dovrà essere
D(λ) = |A - λIn)| = 0
per esempio per n = 2 definendo la matrice come

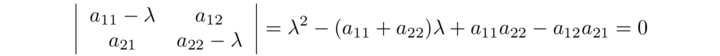
L'equazione (1.0) è un'equazione algebrica in λ di grado n detta equazione caratteristica della matrice A; il polinomio D(λ) è detto polinomio caratteristico della matrice A. Questo polinomio dipende solo dalla trasformazione lineare, e non dal riferimento in cui questa è descritta; in altri termini, non varia se si sostituisce alla matrice A un'altra matrice ad essa equivalente. Infatti si può scrivere
S-1AS - λI =S-1 (A - λI)S
e quindi usando le proprietà del determinante
S-1AS - λI = |S-1 ( A - λI) S| =1 /|S| |A-λI||S| = D(λ)
Chiameremo autovalore della matrice A (o della trasformazione che la matrice A rappresenta) qualsiasi numero λ ∈ ℂ soddisfi l'equazione caratteristica; chiamaeremo autovalore (corrispondente all'autovalore λ) ogni vettore v ≠ 0 (v ∈ 𝕂n)
Notiamo subito che, mentre un autovettore corrisponde sempre ad un unico autovalore (perchè l'identità Av = λ v determina univocamente λ) ad un autovalore corrispondono sempre infiniti autovettori, in quanto se Av = λv, è anche A c v = λ (cv) come già osservato, e quindi tutti i vettori cv paralleli a v sono pure autovettori relativi a λ
Si osservi che, se la matrice A è reale il polinomio caratteristico è a coefficienti reali per cui gli autovalori sono reali oppure a copie complessi coniugati. Gli autovettori posssono essere scelti in modo che agli autovalori reali corrispondano autovettore reali e ad autovalori complessi coniugati corrispondano autovettori complessi coniugati.
Proposizione A.0 Matrici simili hanno lo stesso polinomio caratteristico.
Esempio 1 - Trovare autovalori e autovettori relativi alla matrice

Soluzione - Il polinomio caratteristico è
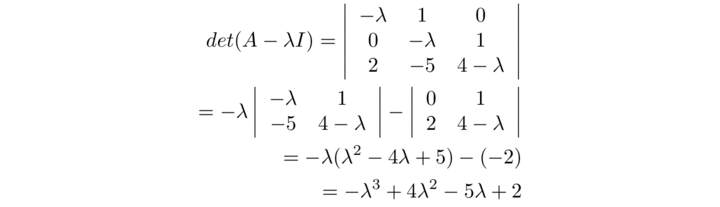
tale polinomio può essere fattorizzato come -( λ - 1)2(λ- 2). Il teorema fondamentale dell'algebra garantisce tre soluzioni che sono λ=1 con molteplicità 2 e λ=2. Per trovare gli autospazi relativi agli autovalori λ1 = λ2 = 1, occorre risolvere il sistema
(A-λI)x = 0
se λ1 =1, E1 = (t, t, t) = span(1,1,1).
se λ1 =2, E2 = (t/4, t/2, t) = span(1/4, 1/2, 1) = span(1, 2, 4).
Definizione Dicesi moleplicità algebrica, mj di un autovalore λ, la molteplicità di λ come radice del polinomio caratteristico.
Quindi nell'esempio precedente λ=1 ha molteplicità algebrica 2 e λ=2 ha molteplicità algebrica 1.
Definizione Dicesi moleplicità geometrica, dj di un autovalore λ, la dimensione dell'autospazio relativo all'autovalore λ, cioè dimEλ.
Nell'esempio precedente entrambi gli autospazi hanno basi formate da un solo vettore dim E1 = dim E2 = 1.
Teorema
Autovettori corrispondenti ad autovalori distinti sono linearmente indipendenti.
La molteplicità geometrica di un autovalore non supera la sua molteplicità algebrica: dj ≤ mj.
Un autovalore si dice regolare se dj = mj. Un autovalore si dice semplice se ha molteplicità algebrica 1. Quando un autovalore è semplice anche dj dovrà essere uguale a 1, perciò un autovalore semplice è sempre regolare