Condizioni di diagonalizzabilità

Teorema D.0 - La matrice A è diagonalizzabile su 𝕂 se e solo 𝕂ⁿ possiede una base di autovettori di A. In tal caso detti p₁, p₂,...,p_n gli autovettori di tale base, e λ₁,λ₂,...,λ_n gli autovalori corrispondenti (λ_i ∈ 𝕂, non necessariamente distinti), risulta

A = SΛS^-1

dove Λ è la matrice diagonale e S = (p₁| p₂|...|p_n) la matrice non singolare che ha per colonne gli auvettori della base.

Dimostrazione - Se la matrice A è diagonalizzabile su 𝕂 vale A = SΛS^-1 che può riscriversi come

AS = SΛ

Tale relazione può riscriversi come Ap_i = λ_ip_i (i= 1, 2,...n). Questo prova che p_i sono autovettori e λ_i sono gli autovalori corrispondenti. Poichè S è una matrice non singolare, i vettori p_i sono indipendenti e quindi sono effettivamente una base di 𝕂ⁿ di autovettori.

Viceversa supponendo che esista una bas di 𝕂ⁿ di autovettori allora le relazioni Ap_i = λ_ip_i si riscrivono come AS = SΛ cioè A = SΛS^-1 perciò A è diagonalizzabile.□

Esempio - Trovare la matrice di passaggio S che diagonalizza

Soluzione - L'equazione secolare risulta essere

(λ - 1) (λ - 2)² = 0

si trovano i seguenti autovettori

λ = 2: p₁ =(-1, 0, 1), p₂ = (0,1,0);

λ = 1: p₃ =(-2, 1, 1)

Ci sono tre vettori nella base quindi la matrice

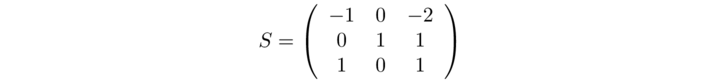
verifichiamo che tale matrice è in grado di diagonalizzare A, ottendo la matrice diagonale seguente

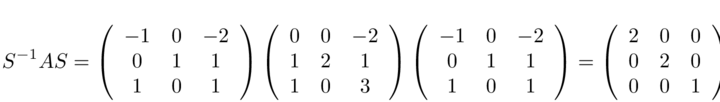
non c'è un ordine di preferenza con cui formare le colonne di S.

Definizione - Una matrice A reale di tipo (n,n) si dice ortogonale se

A ⋅ A^T = A^T A = I

Teorema D.1 - Valgono le seguenti proprietà per matrici ortogonali

1. A è una matrice ortogonale di tipo (n,n) se e solo se le sue righe (colonne) sono una base ortonormale di ℝⁿ.

2. Il determinante di una matrice ortogonale vale 1 o -1

3. Il prodotto di due matrici ortogonali è ortogonale

4. La trasformazione lineare rappresentata da una matrice ortogonale conserva il modulo dei vettori: |Abx| =|x| per ogni x ∈ ℝⁿ, e conserva il loro prodotto scalare: Ax ⋅ Ay = x ⋅ y

Dimostrazione

1. Ricordiamo che la trasporta A^T è quella che si ottiene scambiando le righe con le colonne. Perciò se A=(a_ij), A^T = (a_ji). La relazione A ⋅ A^T = A^T A = I , implica ragionando sugli elementi

   

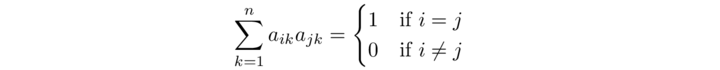
   o in forma più compatta

   a_i⋅ a_j = δ_ij

   ciò significa che i vettori riga di A sono ortonormali (quindi una base essendo di numero n).

2. Dalla relazione A^T ⋅ A = I per il teorema di Binet

   det (A^T) = det (A) si ha det²(A) = 1, det(A) = ±1

3. Siano A,B ortogonali

   (AB) ⋅ (AB)^T = (AB)⋅(B^TA^T) = A (BB^T)A^T =AI_nA^T = AA^T = I_n

   Analogamente si prova che (AB)^T ⋅ (AB) =I_n, perciò AB è ortogonale.

Teorema D.2 - Sia A una matrice reale e simmetrica. Allora A è diagonalizzabile, con una matrice di passaggio ortogonale, ossia

A = MΔM^T

con Δ diagonale e M ortogonale. In particolare, ciò significa che ℝⁿ possiede una base ortonormale di autovettori di A.