Equivalence of Kelvin-Planck and Clausius statements

We have studied the Kelvin-Planck and Clausius statements of the second law of thermodyanamics, the frsit refers to a heat engine and the latter refers to a refrigerator or heat pump: They can be stated as follows

Kelvin-Planck. It is impossible for any device that operates in a cycle to receive heat from a single reservoir and produce a net amount of work.

violazione kelvin-Planck
Fig 1. Such a machine violates the Kelvin-Planck postulate

Clausisu. A transformation whose only final result is to transfer heat from a body at a given temperature to a body at a higher temperature is impossible.

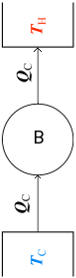
violation Clausius statement
Fig 2. A machine that violates the Clausius statement

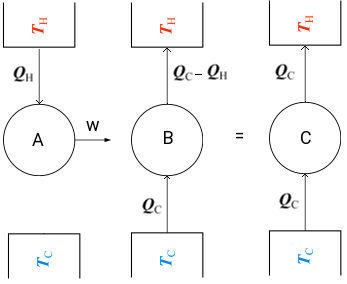
Though it is hard to immediately see any commonality between the Clausius and Kelvin-Planck postulates, we shall prove that both are completely equivalent. In order to demonstrate their equivalence consider the following diagram. On the left we see a machine pump which violates the Kelvin-Planck postulate by transforming all heat, QH into work. This work output of the heat engine can be used to drive a refrigerator, which absorbs an amount of heat QC from a cold reservoir TC and transmits an amount of heat (QC − QH) to an hot reservoir at TH. If hte combination of the heat engine and the refrigerator is considered as a single sytem, as shown, then the result is a device that operates in a cycle and has no effect on the surroundings other thatn the transfer of heat QC from a cold reservoir to the higher temperature reservoir, violating Clausius statement.

violation Clausius statement of the 2nd law
Fig 3. A violation of Kelvin-Planck statement leads to a violation of the Clausius statement

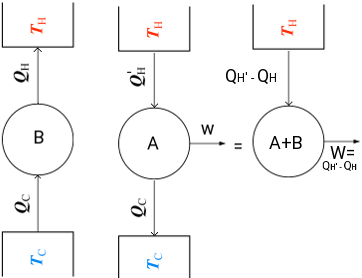
Consider now the system shown in Fig. 4. In this system, a refrigerator is violating the Clausius statement as it transfers heat from a low temperature reservoir at TC to a high temperature reservoir at TH without any expenditure of work. Now let a heat engine, operating between the same heat reservoirs, receives an amount of heat QH' from a high temperature reservoir at TH, does work (W = QH' − QC) and rejectts an amount of heat QC to the low temperature reservoir at TC. The combination of the refrigerator and heat engine is considered as a single system, as shown in Fig.3, then the result is a device that operated in a cycle whose sole effect is to remove heat at the (Qh − QH') and convert it completely into an equivalent amount of work, thus violating the Kelvin-Planck statement.

violation Kelvin-Planck statement of the 2nd law
Fig 4. A violation of Clausius statement leads to a violation of the Kelvin-Planck statement

The Kelvin-Planck and Clausius statements of the second law are thus seen to be equivalent.

«Refrigerators and heat Pumps; Index Carnot's theorem »