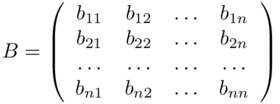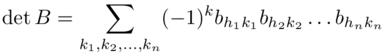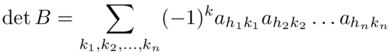Determinant

The determinant is a very important scalar function defined on square n × n real matrices.

which associates a determined number determinante, to a square matrix.

Definition D.0 - Let A = (a_ij) ∈ M_n,n(𝕂) a square matrix of order n with coefficients in 𝕂. The determinant of A is defined as

$$detA=\sum _{\sigma \in S_n}\text{sgn}(\sigma )a_{1\sigma (1)}{a}_{2\sigma (2)}\dots a_{n\sigma (n)}$$

The sum goes over all n! permutations σ of n numbers 1, 2, ..., n, and these permutations form the symmetric group S_n.

sign σ =		1	if σ is an even permutation
		−1	if σ is an odd permutation

while σ(i), i = 1, 2, ..., n, is the image of i under the permutation σ.

As an example we calculate the determinant for small values of n. If n = 1, that is the matrix is composed by a signle element, A = a₁₁, we have det A = a₁₁ (the only permutation is the identity permutation, with sign 1).

For n = 2, we have

$$A=\left(\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right)$$

there are two permutations of two elements

$${\sigma }_1=\left(\begin{array}{cc}1& 2\\ 1& 2\end{array}\right),{\sigma }_2=\left(\begin{array}{cc}1& 2\\ 2& 1\end{array}\right)$$

Si ha sgn(σ₁) = 1 e sgn(σ₂) = −1, per cui il determinante è lo scalare

As last example we consider the case n = 3. There are 3! = 6 permutations of three elements, namely

$$\begin{array}{rlrlrl}{\sigma }_1& =\left(\begin{array}{ccc}1& 2& 3\\ 1& 2& 3\end{array}\right)& {\sigma }_2& =\left(\begin{array}{ccc}1& 2& 3\\ 1& 3& 2\end{array}\right)& {\sigma }_3& =\left(\begin{array}{ccc}1& 2& 3\\ 1& 2& 3\end{array}\right),\\ {\sigma }_4& =\left(\begin{array}{ccc}1& 2& 3\\ 2& 1& 3\end{array}\right)& {\sigma }_5& =\left(\begin{array}{ccc}1& 2& 3\\ 3& 1& 2\end{array}\right)& {\sigma }_6& =\left(\begin{array}{ccc}1& 2& 3\\ 3& 2& 1\end{array}\right)\end{array}$$

Si verifica facilmente che sgn(σ₁) = sgn(σ₃) = sgn(σ₅) = 1, mentre sgn(σ₂) = sgn(σ₄) = sgn(σ₆) = −1, quindi

As n increases the determinant of n x n matrix is complicated to be calculated directly, from the definition. We shall see other methods which are not based on the definition of determinant.

From the definition some properties which can be easily verified follow.

Proposition D.0 - The determinant of any triangular matrix A (lower, upper, or diagonal) is the product of all diagonal elements: det A = a₁₁a₂₂a_nn

Proof. Dato che A = (a_ij) è una matrice triangolare superiore, si ha a_ij = 0 if i > j. We observe that for every permutation σ of {1, 2, ..., n}, different from id, there exists an index i such that i > σ(i). The product a_1σ(1) a_2σ(2) ··· a_nσ(n) is thus zero, given the fact that at least one of its factors is zero. Hence the only permutation giving a non-null addend is id, thus it results det A = a₁₁a₂₂ a_nn.  □

Proposition D.2 - For any square matrix A, we have det A^T = det A, or, in other words, the matrix A and its transpose have equal determinants.

Proof. We have

per la definizione di determinante si può scrivere:

given Eq. (1.3) we have:

Il secondo membro della presecente non è altro che det A. La proposizione è così dimostrata.□