Laplace's theorem

In this section we study the Laplace expansion, which is the classical way of calculating an n x n determinant as a sum of (n − 1) x (n − 1) determinant.

Consider an arbitrary n x n matrix. For any element i,j imagine the deletion of the rwo and column containing the (i,j)th entry of A to leave a (n − 1) x (n − 1) matrix: the determinant of this (n − 1) x (n − 1) submatrix is called the minor of the (i,j)th entry of A and will be denoted by M_ij. Hence M_i,j = det A_{i, j}, where A_i,j is the minor matrix in A

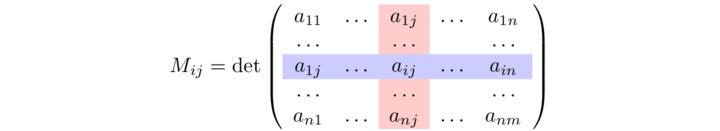
From this we can define the cofactor or signed minor, c_i,j.

c_ij = (−1)^i+j M_ij

For example taking the elements a₁₁, a₁₂, a₁₃, the signs of cofactors are (−1)¹⁺¹ , (−1)¹⁺², (−1)¹⁺³, i.e., (−1) to the power which is the sum of indices of the elements from the first row.

Il teorema di Laplace o sviluppo di Laplace, il cui nome è dovuto a Pierre Simon Laplace, è una formula che permette di calcolare il determinante di una matrice (quadrata) con un procedimento ricorsivo. Lo sviluppo può essere eseguito per righe oppure per colonne. Il primo teorema di Laplace afferma che il determinante di una matrice quadrata A di ordine n è pari alla somma dei prodotti degli elementi di una riga qualsiasi (o una colonna qualsiasi) per i rispettivi complementi algebrici.

First Laplace's theorem - The determinant det A of an n × n matrix A can be computed by multiplying the entries of any row or any column by their respective cofactors and adding the resulting product. More precisely:

det A = ∑ⁿ_{_i=1} a_ijc_ij (1.3)

expansion by row

or by fixing the row i.

det A = a_i1c_i1 + a_i2c_i2 + ... + a_inc_in

We prove the theorem having fixed columns, c₁, ..., c_n of the matrix A. THe j-th colum can be written as c_j = a_1je₁ + ... + a_nje_n. Thus

|A| = det (c₁, ..., c_j, ..., c_n) = ∑ⁿ_{_i=1} a_ij det (c₁,...,e_i,... c_n).

with n − j changes of places we can take the j-colunmn to the last position leaving the rest unchanges. With n − i changes we can take the i-th row to the last position leaving unchanged the order of the other rows. Thus

|A| = ∑ⁿ_{_i=1} (-1)^n-j a_ij det (c₁,..., c*_j,..., c_n, e_i) = ∑ⁿ_{_i=1} (-1)^n-j (-1)^n-1 a_ij det (c₁ⁱ,..., c*_j,..., c_nⁱ, e_i)

where c*_j means that the j-th column does not appear. Owing to proposition 36 we have

|A| = ∑ⁿ_{_i=1} (-1)^i+j a_ij det (c₁ⁱ,..., c*_j,..., c_nⁱ)

where det (c₁ⁱ,..., c*_j,..., c_nⁱ) is determinant of the matrix obtained elimininating from A the i-th row and j-th column. Thus we have (-1)^i+j det (c₁ⁱ,..., c*_j,..., c_nⁱ) = A_ij. □

La regola di Laplace sfrutta il complemento algebrico fornendo un comodo merodo iterativo per calcolare un determinante qualsiasi: si sceglie arbitrariamente una riga (o una colonna) e si moltiplicano per i corrispondenti complementi algebrici tutti gli elmenti della matrice che si incontrano scorrendo quella riga (o quella colonna).

Esempio 1- Applichiamo il teorema di Laplace per calcolare il determinante della matrice

osserviamo innanzitutto che, poichè la matrice ha un elemento nullo, risulta conveniente effettuare il calcolo rispetto ad una riga o una colonna che contenga lo zero; sviluppando ad esempio rispetto alla seconda riga risulta:

det (A) = -4 (7*4 - 15) + 0 (14 - 25) +3 (-6 + 20) = -52 + 42 = -10

Dalla definizione di determinante seguono delle proprietà di facile verifica:

Proposizione D.1 - Se in una matrice quadrate A, sono nulli tutti gli elementi di una riga (o di una colonna) si ha det A=0.

Proposizione D.2 - Se A^T è la matrice trasposta della matrice qudrata A, si ha:

Dim. Se A è la matrice, indichiamo la trasposta con:

per definizone di A^T:

(1.3)

per la definizione di determinante si può scrivere:

data la (1.3) si ha:

Il secondo membro della presecente non è altro che det A. La proposizione è così dimostrata.□

Teorema D.0 - Operando una sostituzione nelle righe (o colonne) della matrice A, si ottiene una matrice B, tale da aversi:

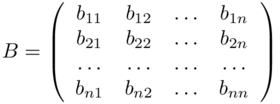
avente determinante pari a:

dove h è uguale al numero delle inversioni della permutazione generica h₁, h₂, ..., h_n

Dim. La sostituzione è tale da aversi:

B matrice sostituita (1.4)

con r =1, 2,...,n. Per la (1.2) si ha:

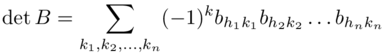
che per la (1.4) può scriversi come:

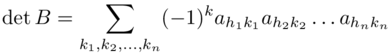
il secondo membro dell'ultima equazione vale per la (1.2) (-1)^h det A, si ha quindi la tesi:

□

Secondo Teorema di Laplace - Data una matrice quadrata A, la somma la somma dei prodotti degli elementi di una riga (o colonna) per i complementi algebrici di un'altra riga (o colonna) della matrice stessa è sempre nulla.

Dimostrazione - Il motivo di tale risultato è hce in questi casi si sta calcolando il determinante di una matrice con due righe o due colonne uguali, per cui il determinante è nullo.

«Thermodynamic Systems Index Teorema di Binet, Regola di Sarrus »