Simple Extensions

We shall se now how given a field F and one of its extension K, is possible to obtain intermidiate extensions between K and F. Usually if you just add a random element to a field, you lose the closure property and the inverse property unless you also add a whole slew of other elements; thus we follow a different path.
Starting with a field F and a subfield K. If u ∈ F, what can be said about the subfields of F that contain both u and K? Is there a smallest such subfield? The answer to the first two questions is quite easy. Let F be an extension field of K and u ∈ F. Let K(u) denote the intersection of all subfields of F that contain both K and u (this family of subfields is nonempty since F at least is in it). Since the intersection of any family of subfields of F is itself a field (Exercise 1), K(u) is a field. By its definition, K(u) is contained in every subfield of F that contains K and u, and, hence, K(u) is the smallest subfield of F containing K and u. K(u) is said to be a simple extension of K.
It turns out that the structure of K(u) depends on whether or not u is the root of some polynomial in F[x].

Definition 8.2.1. Let F a field, and let a₁, a₂, ..., a_n be elements of some extension E of F. We use F(a₁, a₂, ..., a_n) to denote the smallest subfield of E that contains F and the set {a₁, a₂, ..., a_n}. Next theorem shows that F(a₁, a₂, ..., a_n) is the intersection of all subfields of E that contain F and the set {a₁, a₂, ..., a_n}.

Let K an extension of F and let S a subset of K. We indicate as

Then it results

In addition F(S) is the quotient field of F[S]. On the other hand, a union of subfields is not in general a subfield as the following figure shows

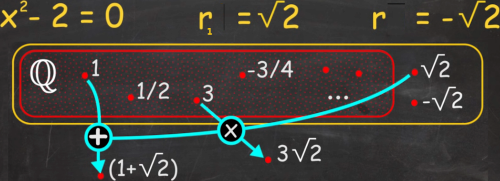
Example 8.2.2. Let F be any field and let x₁, ..., x_n be independent variables. The polynomial ring F[x₁, ..., x_n] is an integral domain (see Proposition 4.3). The quotient field of F[x₁, ..., x_n] is denoted F(x₁, ..., x_n). It consists of all fractions f/g, with f,g ∈ F[x₁, ..., x_n] and g ≠ 0, and the usual addition and multiplication. Then F(x) is an extension of F. ■

We now want to know which are the elements of F(S). We start by adding a single elements to a field F, i.e we study the case S = {a} that is F(S) is a simple extension. The standard procedure for constructing the complex numbers from the real numbers is to ‘adjoin’ a square root of −1; that is, an element i satisfying i² + 1 = 0. We will now describe this procedure, ‘adjoining the root of a polynomial’, in more detail.

8.2.3 Proposition. Let K an extension of F and let a ∈ K. Then F(a) = T where T is the defined as the set

Proof. Given an extension field K of F and an element a ∈ K, any subfield that contains F and a must be closed under sums and products, so it must contain all elements of the form α₀ + α₁ a + ... + α_naⁿ, where α_i ∈ F for 0 ≤ i ≤ n. Furthermore, since it must be closed under division, it must contain all elements of the form

such that the denominator is nonzero. We clearly have

since that T is a field containing F and a. The reverse inclusion holds as well, F(a) ⊆ T, since the elements of T must be contained in every field containing F and a.  □

Example 8.2.4. Let F = ℚ, K = ℝ and a = π, then

ℚ(π) means the smallest possible subfield of ℝ containing π and all ℚ. Notice how ℚ is a field, but the set ℚ ∪ {π} is not even a ring, much less a field.  ■

Example 8.2.5. Let F = ℚ, K = ℝ and a = √3, then

However given that √3² = 3, the expressions inside ℚ(√3) can be reduced to

But

and

are bot elements of ℚ. Thus the elements of ℚ(√3) can be all be written in the form q₀ + q₁ √3, with q₀, q₁ ∈ ℚ. Then

In the last case we have seen that the extension can be simplified, whilst in the first case it wasn't possible. The reason behind this behavior lies down to the specific nature of the element a we are adjoining.

Definition 8.2.14. Let K be an extension field of F and let a ∈ K. If there exists a nonzero polynomial f(x) ∈ F[x] such that f(a) = 0, then a is said to satisfy the polynomial f(x) and to be algebraic over F. Otherwise, a is said transcendental over F.  □

Remark. When a real number is called transcendental, it usually means that it is transcendental over ℚ. For example, it was proved by Lindemann that π is a transcendental number; there is no nozero f(x) ∈ ℚ[x] with f(π) = 0. I numeri trascendenti sono numeri irrazionali che non sono radici di alcun polinomio a coefficienti razionali. Ossia un numero trascendente è un numero reale che non è soluzione di alcuna equazione polinomiale della forma

dove n è un numero naturale maggiore di zero ed i coefficienti a_i sono numeri razionali non tutti nulli. ■

Example 8.2.6. For instance, the number √2 is an element of ℝ that is algebraic over ℚ, because it is a root of x² − 2 ∈ ℚ[x]. Of course, √2 is also a zero of x³ − 2x and of x⁴ − 3x² + 2 = (x² − 2)(x² − 1). Both these other polynomials having 2 as a zero were multiples of x² − 2. Another example is ∛2 and (4 + √2)^1/5 are algebraic over ℚ since they are zeros of x³ − 2 and (x⁵ − 4)² − 2 respectively. ■

Example 8.2.7. In the extension field ℂ of ℝ, i is algebraic over ℝ because i is the root of x² + 1 ∈ ℝ[x]. You can easily verify that element 2 + i of ℂ is a root of x³ − x² − 7x + 15 ∈ ℚ[x]. Thus 2 + i is algebraic over 0.  ■

Example 8.2.8. Every element c in a field F is algebraic over F because c is the root of x − c ∈ F[x].  ■

The familiar constants e and π are transcendental over ℚ. The analytic proofs lie beyond the scope of this book. That e is transcendental was proved by Charles Hermite (1822–1882) in 1873, and the corresponding result for π was proved by the German mathematician Ferdinand Lindemann (1852–1939) in 1882. It is well known that e^π is transcendental, while it is not known the nature of π^e.

Theorem 8.2.9. Let F a field and K an extension of F. Let a ∈ K, the mapping

is a ring homomorphism with Im Ψ_a = F[a] known as the evaluation homomorphism.

Proof. For every f,g ∈ F[x] it results

Thus this is a ring homomorphism.

The image of the homomorhism Im Ψ_a is a subring of K which contains F and a, thus it contains F[a]. On the other hand, if t is an element in Im Ψ_a, then t = Ψ_a(f) for some f ∈ F[x]. If

then

thus Im Ψ_a = F[a]. □

Corollary 8.2.10. Let F a field and let K an extension of F. Given a ∈ K and Ψ_a the evaluation homomorphism, a results algebraic if and only if Ker Ψ_a ≠ 0 (thus a is transcendental if and only if Ker Ψ_a ≠ 0).

Theorem 8.2.11. Let F a field, K an extension of F and a transcendental over F, then there exists an isomorphism between F(a) and the field of rational functions F(x) with coefficient in F. In particular, [F(a) : F] is infinite.

Proof. From theorem 8.2.9, corollary 8.2.10 and the fundamental homomorphism ring theorem, follows that

Then their quotient fields are isomorphic as well, i.e.:

[F(a) : F] is infinite because: 1, a, a², ..., aⁱ, ... are linearly independent over F.  □

Remark. The vectors 1 = a⁰, a, a², ..., aⁱ are linearly independent only when a is transcendental. If a were algebraic over F, e.g. consider the algebraic a = √2, over the reals, we'd have a² − 2 = 0, which is linear dependent combinations of powers. □

Thus if K is an extension of F, all the extension of F(a) with a transcendental over F are mutually isomorphic; the element a can be regarded as an unknown x and F(a) can be identified with rational function in the indeterminate x.

Next theorem shows how the finite or infinite nature F(a) over F determines whether a is algebraic or transcendental over F.

Definition 8.2.12. Let K be an extension of a field F. Let α ∈ K be algebraic over F. We define the minimal polynomial of α over F as the unique monic, irreducible polynomial p in F[x] that has α as a root. □

8.2.13 Theorem. Let K an extension F and let a an algebraic element over F. Then, if Ψ_a is the evaluation homomorphism from F to K,

1. Ker (Ψ_a) = (p(x)) where p(x) is a monic irreducible polynomial in F[x] known as the minimal polynomial of a over F.

2. A polynomial f(x) ∈ F[x] has a zero in a, if and only if p(x) divides f(x);

3. F(a) = F[a] and F(a) ≃ F[x]/(p(x));

4. [F(a) : F] = deg p(x) and F(a) has basis 1, a, a², ..., a^{n − 1}

Proof.

1. From the fundamental theorem on ring homomorphism, we have

   F[a] ≃ F[x]/ Ker Ψ_a

   Now, F[a] as subring of a field, is an integral domain (see Proposition 6.1.5), hence by Theorem 1.6.11 Ker Ψ_a is a prime ideal hence generated by an irreducible element; The division of this polynomial by its leading coefficient yields a monic polynomial with minimal degree zeroed by a.

2. A polynomial f(x) ∈ F[x] is such that f(a) = 0 if and only if f(x) ∈ Ker Ψ_a and thus if and only if p(x) | f(x).

3. It results F(a) = F[a], since under current hypothesis (Ker Ψ_a is generated by an irreducible element) the quotient F[x]/ Ker Ψ_a, and thus F[a] are fields. Since F[a] contains are F and a, it follows that F[a] = F(a) and F(a) ≃ F[x]/p(x).

4. Let n the degree of p(x). We prove that the element 1, a, a², ..., a^{n − 1} are a basis for F[a] (= F(a)). We prove first the linear independence; Let

   $$\sum _{i=0}^{n-1}{\alpha }_i{a}^i=0,{\alpha }_i\in F$$

   and consider the polynomial f(x) = ∑^{n − 1}_i=0 α_ixⁱ ∈ F[x]. Since f is a polynomial zeroed by a, it belongs to Ker Ψ_a, thus a multiple of p(x) (by point a) being a zero of f is the same as being in Ker(Ψ_a), and this is the ideal ⟨p(x⟩ which is exactly all the multiples in F[x] of the polynomial p(x)).
   Being, n the degree of p(x), whilst n − 1 that of f(x), f(x) must necessarily be a null polynomial thus all the α_i must be null. The linear independence of 1, a, a², ..., a^{n − 1} is thus proved. We now prove that the 1, a, a², ..., a^{n − 1} are generators of F[x]. If s is an element of F[a], there exists a polynomial f(x) ∈ F[x], such that s = Ψ_a(f(x)) = f(a). Dividing f(x) by p(x) we obtain

   f(x) = q(x)p(x) + r(x),   r = 0 or deg(r(x)) < deg(p(x))

   Evaluating the relation in a we obtain

   f(a) = q(a)p(a) + r(x) = q(a) ⋅ 0 = r(a)

   We managed to express s = f(a) as linear combination of elements 1, a, a², ..., a^{n − 1}, which are thus generators.  □

Notice how the writing f(a) = α₀ + α₁a + α₂ a² + ... + α_{n −1}a^{n − 1} of every element F[a] is unique, since the elements 1, a, a², ..., a^{n − 1} represent a basis.

8.2.14 Corollary. Let K an extension of the field F and let a ∈ K. Then a is algebraic if and only if F(a) is a finite extension, whilst is transcendental if and only if F(a) is an infinite extension.

Proof. If a is transcendental, by theorem 8.2.11 we know that F[x] ≃ F(a), and [F(a) : F] is infinite because: 1, a, a², ..., aⁱ, ... are linearly independent over F.

If a is algebraic, by theorem 8.2.13(c) we know that in this case F[a] is a field such that F[a] = F(a). The minimal polynomial has degree n = [F(a) : F] and F(a) has the finite basis: 1, a, a², ..., a^{n − 1}.  □

Nota bene: "simple" doesn't mean finite in the sense of degree, = vector-space dimension. ℚ(π) is a simple extension of ℚ, since {π} has just one element, but it's infinite-dimensional since π is transcendental.

8.2.15 Example. We've thus characterized simple extensions. Suppose now to build the extension ℚ(S), with S = {√3, √5} and calculate its degree in ℚ. We proceed in this way: we adjoin first √3 obtaining the extension ℚ(√3) and then adjoin the element √5 to ℚ(√3). With the aid of theorem 8.2.16 we can easily calculate the degree of the extension. √3 is algebraic over ℚ, of degree 2 since its minimal polynomial is x² − 3; By theorem 8.2.16 ℚ(√3) ≃ ℚ([x]/(x² − 3). We now adjoin √5 to ℚ(√3). The polynomial x² − 5 is irreducible (not only over ℚ, but also) over ℚ(√3) (Why? see the exercises). Thus the extension ℚ(√3,√5) = (ℚ(√3))(√5) has degree two over ℚ(√3). Then by theorem 8.2.4 we have

Since a basis of ℚ(√3,√5) over ℚ(√3) is {1, √5} and a basis over ℚ(√3) over ℚ is {1,√3}, a basis of ℚ(√3,√5) over ℚ is given (se theorem ) by