Fundamental theorem of ring homorpshims and isomorphism

6.5.1 Proposition (Fundamental theorem of ring homomorphism) Let R and R' two rings and let f: R ⟶ R' an homomorphsim between rings. Then there exists a unique isomorphim f* from R/Ker f to Imf

such that f* ∘ π = f, with π the canonical projection of R on R/Ker f.

Proof. If f* has to satisfy f = f* ∘ π, we must define it as follows

we now must check that

1. f* is well-defined, i.e. if [x] = [y] ⇒ f(x) = f(y)

2. f* is bijective.

3. f* is an homomorphism.

1. [x] = [y] ⇐⇒ x − y ∈ Ker f ⇐⇒ f(x − y) = 0 ⇐⇒ f(x) = f(y). Double implications prove at the same time that f* is well-defined and injective.

2. It is left to prove that f* is surjective: An element f(x) ∈ Imf, has counter image x ∈ R. And an element [x] is mapped through f* to f(x), hence f* is surjective Imf* = Imf.

3. f*([x] + [y]) = f*([x + y]) = f(x+y) = (being f an homomorphism) = f(x) + f(y) = f*([x]) + f*([y]). Analogously for the product.

It follows naturally from the definition of f* that f = f* ∘ π.

The theorem can be depicted in the following diagram.

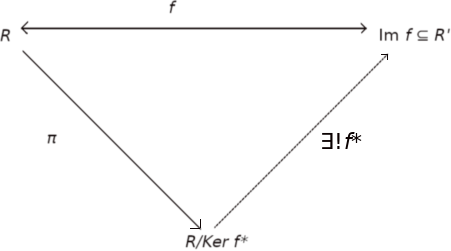
This diagram tell us that there exist only one isomorphism f*, from R/Ker f to Im f for diagram to be commutative, that is such that f = f* ∘ π.□

If there exists an homomorphism f of R onto R', then R' is called an isomorphic image of R.

The theorem states that every homomorphic image of a ring R is isomorphic to a quotient ring R/I for some ideal I. Thus if you know all the quotient rings of R, then you know all the possible homomorphic images of R. The ideal I measures how much information is lost in passing from the ring R to the homomorphic image R/I.

Moreover to prove that a quotient ring R/I is isomorphic to a ring R' it is sufficient to find an epimorphism φ from R' to R such that I = Ker φ.

6.5.2 Example Consider ℤ, the ring of integers and let n > 1 be a fixed integer and let I_n (= nℤ) be the set of all multiples of n; then I_n is an ideal of ℤ. If ℤ_n, is the integers mod n, define φ: ℤ ⟶ ℤ_n, by φ(a) = [a]. As is easily seen, φ is a homomorphism of ℤ onto ℤ_n, with kernel I_n. So by the Fundamental theorem of ring homomorphism, ℤ_n ≃ ℤ/I_n. (This should come as no surprise, for that is how we originally introduced ℤ_n.)

6.5.2 Proposition Let f an homomorphism between two rings R and R'. Then

1. if A is a subring of R, f(A) is a subring of R'.

2. if I is an ideal of R, f(I) is a ideal of f(R) (= Im f) (not necessarily of R').

3. if A' is a subring of R', f⁻¹(A') is a subring of R containing Ker f.

4. if I' is a an ideal of R', f⁻¹(I') is an ideal of R containing Ker f.

Note f⁻¹(A') here means the preimage or "inverse image" i.e. the set {r ∈ R: f(r) ∈ A'}.

Proof.

1. Given two elements f(a) and f(a̅) of f(A), we have f(a) − f(a̅) = f(a − a̅) ∈ f(A) and f(a)f(a̅) = f(aa̅) ∈ f(I) since a − a̅ ∈ A and aa̅ ∈ A.

2. It is sufficient to prove that f(a)f(x) ∈ f(I) and f(x)f(a) ∈ f(I) because ax ∈ I. Analogously f(x)f(a) ∈ f(I).

3. Let a, a̅ ∈ f⁻¹(A'), such that f(a) ∈ A' and f(a̅) ∈ A'. Then f(a − a̅) = f(a) − f(a̅) ∈ A', and f(aa̅) = f(a)f(a̅) ∈ A' hence a − a̅ and aa̅ are in f⁻¹(A'). The last element contains Ker f, since ∀k ∈ Ker f, f(k) = 0_R', which is contained in every ring A'.

4. Let x ∈ R and a ∈ f⁻¹(I'). We must prove that xa and ax are in f⁻¹(I'). Indeed, f(xa) = f(x)f(a) ∈ I' (since f(a) ∈ I'). Analogously f(ax) ∈ I'. In this case as well f⁻¹(I') contains Ker f.□

6.5.3. Example. Let R = ℤ and R' = ℤ₄ = ℤ/4ℤ, and f = π the canonical projection of ℤ on ℤ/4ℤ. Let A = 6ℤ. The elements of 6ℤ are distributed in only two classes of ℤ modulo 4ℤ. Considering the quotient modulo I = 4ℤ.

6ℤ + 4ℤ = {a + b | a in 6ℤ, b in 4ℤ}. For that, the mean the multiples of 6 in ℤ fall into only two of the four possible cosets of 4ℤ. In other words, out of the possible values 0,1,2,3 for what some n in ℤ can be mod 4, only two of those values come up when you look at just the n in 6ℤ.

π(A) = 6ℤ/4ℤ = [0, 2] = {I, 2+I}, because, a multiple of 6 divided by 4 can have as remainder either 0 or 2.

R/I = ℤ/4ℤ because every n in ℤ can be written uniquely as 4m + r where r is in {0,1,2,3} by the division algorithm. So R/I = {I, 1+I, 2+I, 3+I}. It's easy to see that π(A) is an ideal of R/I.

6.5.4. Corollary. Let R a ring, I one of its two-sided ideal and π: R ⟶ R/I, the canonical projection. Then

1. S subring (ideal) of R ⇒ π(S) = (S + I)/I is a subring (ideal) of R/I;

2. S subring (ideal) of R/I ⇒ π⁻¹(S') is a subring (ideal) of R containing I.

Proof.

1. let S be a subring of R. π is a homomorphism between R and R/I, so by point 1 of 6.5.1, π(S) is a subring of R/I.

2. let S be an ideal of R. π is a homomorphism between R and R/I, so by point 2 of 6.5.1, π(S) is an ideal of π(R). Furthermore, π defined as r ⟼ r + I is a surjection, so π(R) = R/I. Therefore, π(S) is an ideal of R/I.

On why (S + I)/I = π(S) and π(s) is an element of (S + I)/I, π(s) = s + I by definition. Anything in (S + I)/I is some coset x + I where x is in the set S + I, so x is some s + i (s ∈ S, i ∈ I), so x + I = s + i + I = s + I = pi(s). Conversely, take any π(s) in π(S). π(s) = s + I = s + i + I with i = 0 in I.□

6.5.6. Example. Determine all ideals of the quotient ring ℤ/12ℤ.

The ring is now made of elements of the sort z + 12ℤ with z ∈ ℤ. We must find (z + 12ℤ)(i + 12ℤ) = zi + 12ℤ. Using the correspondence theorem, find all ideals of ℤ containing 12ℤ and then use the Ψ to create the correspondence with the ideals of ℤ/12ℤ. For example if we take even numbers 2ℤ this is an ideal of 6.5. since an even number multiplied by an integer is again even: 12ℤ ⊂ 2ℤ. We have that mℤ ⊂ nℤ iff n | m, so these sets are

Then the ideals of ℤ/12ℤ are

12ℤ/12ℤ: this set is nothing but {12ℤ}.

6.5.6. Theorem. (First Isomorphism theorem) Let R a ring, I one of its ideal and π the canonical projection. Let A a subring of R not necessarily containing I. Then

1. π⁻¹(π(A)) = A + I = {a + i | a ∈ A, i ∈ I}

2. A ∩ I is an ideal of A and I is an ideal of A + I.

3. A/(A ∩ I) ≃ (A + I)/I.

Proof.

1. We have π⁻¹(π(A)) ⊇ A for all functions. A stronger statement is π⁻¹(π(A)) ⊇ A + ker π, because

   π(a + z) = π(a) + π(z) = π(a) when π(z) = 0, i.e. z ∈ ker π.

   Then π⁻¹(π(A)) = A + ker(π) and ker(π) = I, so π⁻¹(π(A)) = A + I;

2. I is an additive subgroup, and i(a + i) ∈ I since both ai and ii are in I (because I is an ideal of R and a ∈ R. A ∩ I is an additive subgroup: if x,y ∈ A ∩ I then x and y are in A, so x + y is in A and x and y are in I, so x + y is in I that is A ∩ I is an additive subgroup. Moreover xa ∈ A since A is an ideal of R

3. If π: R ⟶ R/I, let π_|A the restriction of π to A that is

   π_|A: A ⟶ (A + I)/I

   It is a ring homomorpshim whose kernel is

   Ker π_|A = {x ∈ A | π_|A (x) = I} = {x ∈ A | x + I = I} = A ∩ I}

   The result follows by virtue of the fundamental theorem of ring homomorphism.□

6.5.7. Theorem. (Second Isomorphism theorem) Ler R a ring, I and J two ideals of R such that I ⊆ J. Then

Proof. Based on the fundamental ring homomorphism theorem, it is sufficient to prove the existence of a an epimorphosm of rings from R to (R/I)/(J/I) with kernel J. The composite function π = π₂ ∘ π₁ of canonical projections

is an epimorphism of R to (R/I)/(J/I), we have

Ker π = {r ∈ R | π₁(r) ∈ Ker π₂ = {r ∈ R | r + I = j + i, j ∈ J} = J.

Ker π is composed by elements elements r ∈ R such that π₂(r + I) = 0 is satisfied. The 0 element of (R/I)/(J/I) is J/I. The elements of J/I are j + I.

The isomorphism f: R/J ⟶ (R/I)/(J/I) is defined as follows f(r+J) := (r + I) + J/I.□

Example 6.5.8. Determine the isomorphism for the case R = ℤ, I = 12ℤ and J = 3ℤ.

Solution. We have 12ℤ ⊂ 3ℤ since every multiple of 12 is a multiple of 3. We have also

The ideal 3ℤ/12ℤ of the ring ℤ/12ℤ consists by definition of those residue classes of ℤ/12ℤ whose representatives are in 3ℤ, i.e, multiples of 3. We see that

Finally, we have

There are repretitions among these twelve elements: two residue classes (m₁ + 12ℤ) + 3ℤ/12ℤ and (m₂ + 12ℤ) + 3ℤ/12ℤ are equal iff

So the ring (ℤ/12ℤ ) /(3ℤ/12ℤ ) really consists of just the threee residue classes

We have thus confirmed the statement of the second isomorphism theorem:

Using the second isomorphism theorem, we have the isomorphism f: ℤ/J ⟶ (ℤ/I)/(J/I) is defined as follows f(r + J) := (r + I) + J/I which for this case is f(m + 3ℤ) := (r + 12ℤ) + 3ℤ/12ℤ. Thus

[3]₁₂ just refers to that specific element of the 12-element ring ℤ₁₂, and then [3]₁₂ℤ₁₂ means the set of all products [3]₁₂(n_{12}) in this ring namely {[0]₁₂, [3]₁₂, [6]₁₂, [9]₁₂}.