Sets
The notions of sets and numbers are ancient. The first rigorous definition of the set of real numbers (1871) is attributed to George Cantor (1845–1918).
We assume as primitive the notion of set (we must accept without definition some terms that are basic objects in our mathematical systems). Suppose, we define the term set as “A set is a well-defined collection of objects.” One naturally asks what is meant by a collection. We could define it as “A collection is an aggregate of things.” What, then, is an aggregate? Now our language is finite, so after some time we will run out of new words to use and have to repeat some words already examined. The definition is then circular and obviously worthless. Mathematicians realize that there must be some undefined or primitive concept with which to start. At the moment, they have agreed that set shall be such a primitive concept. We shall not define set, but shall just hope that when such expressions as “the set of all natural numbers” or “the set of all students of a school” are used, people’s various ideas of what is meant are sufficiently similar to make communication feasible.
A set A is a collection of objects named elements, about which it is possible to determine whether or not a particular object is a member of the set. Sets are usually denoted by capital letters A, B, X, ..., and its elements with lower case letters a, b, x, ...
To indicate that a particular element a belongs to the set A, we write
a ∈ A
if it does not belong to the set we write
a ∉ A
Sets are usually described by a list of their elements, which are enclosed whithin { }. For example the set A of natural numbers less than 10 can be written as follows:
A = {0,1,2,3,4,5,6,7,8,9,10}
or with set-builder notation using braces to enclose a property that is the qualification for membership in the set.
A = {n ∈ ℕ | n < 10}
The vertical slash is shorthand for “such that,” and we read: A is the set of all n of ℕ such that n is less than 10.
The following are the fundamentals symbols used in mathematics, which allow to write long statements in a concise symbolic way otherwise too long to express:
| Symbol | Meaning |
|---|---|
| ∀ | for “all”, “every”, "each" |
| ∃ (∄) | there exists (there does not exist,) |
| ∃! | there exists one and only one |
| ∈ (∉) | belongs to (does not belong to) |
| ⊆ (⊈) | is a subset (is not a subset) |
| ⊂ (⊊) | is properly contained |
| ⇒ (⇏) | implies (does not implies) |
| ⇔ | if and only if |
| | o : | such that |
| := | equal by definition |
| ⇐⇒ and the word “iff” | both mean “if and only if.” |
| v | o (inclusivo), vel, or |
| ∧ | e, et, and (congiunzione) |
If B is a set whose elements are included in a set A we say that B is included in A or that B subset of A
B ⊆ A
To exclude the possibility of equality between B and A i.e. if there are elements of A not within B we use the notation
A ⊊ B or A ⊂ B
Proper inclusion: The assertion "A ⊊ B" (A is a proper subset of B) means that every element of A is an element of B, but there is at least one element of B that is not an element of A so A ≠ B. Symbolically
A ⊊ B ⇐⇒ [∀a, a ∈ A ⇒ a ∈ B, and ∃b ∈ B | b ≠ A]
For example, ℤ ⊊ ℝ because every integer is a real number but there are real numbers that are not integers.
Two sets are said to be equal, if every element of one set is in the other set and vice-versa, we write
A = B
There is a simple way to show that two sets are equal, to show that A = B, show first that B ⊂ A and then that B ⊃ A. This means that A is included in B and B is included in A and thus arise the term double-inclusion.
The empty set does not contain elements, indicated with ∅, or simply as { }. The empty set is a subset of every set (included itself).
The intersection of two sets A and B is the set of all those elements that belong to both A and B and it is indicated as A ∩ B, symbolically
A ∩ B := {x | x ∈ A and x ∈ B}
Their union of two sets A and B, is the set of elements that belong to either or both of them A ∪ B,
A ∪ B := {x | x ∈ A ∨ x ∈ B}
Example 1.1.1 Let A = {a,b,c,d,e,f} and B = {a, d, l, m, n}. Thus
A ∩ B = {a, d}, A ∪ B = {a, b, c, d, e, f, l, m, n}
If A and B are two sets, the difference set A \ B or A − B, is the set of all elements of A which do not belong to B.
A \ B = {x ∈ A | x ∉ B}
Let now Ω a set containing all the elements of our interest, let's call it universe. We define the complement of a set A (with respect to the universe set Ω) the set of all elements of Ω which do not belong to A. The complement is indicated as AC.
AC := Ω \ A
More formally as
AC := {x ∈ Ω | x ∉ A}
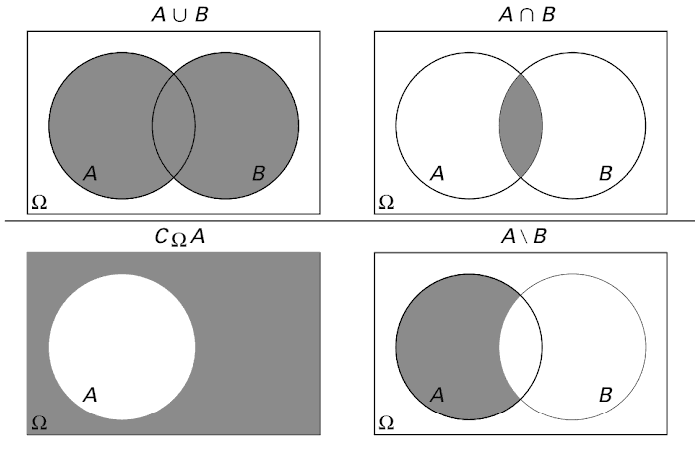
The following are known as Venn's Diagrams, and represent the definitions given above
Properties of set operations
The operations of forming unions, intersections, and complements of events obey certain rules not dissimilar to the rules of algebra. We list a few of these.
Commutative law E ∪ F = F ∪ E
Associative law (E ∪ F) ∪ G = E ∪ (F ∪ G)
Distributive law (E ∪ F)G = EG ∪ FG
There is a resemblance between the properties of the union and intersection with the familiar distributive property x(y + z) = xy + xz for numbers as well for the associative and commutative properties.
To prove the distributive property, we denote the right and left member with E and F respectively. Supposing that x ∈ E. Then x ∈ A and x ∈ B ∪ C i.e. x ∈ B or x ∈ C (possibly both). Thus x ∈ A ∩ B or x ∈ A ∩ C), so that x ∈ F. Thus E ⊂ F. Supposing also that x ∈ F. Then x ∈ A ∩ B or x ∈ A ∩ C, i.e., x ∈ A and x ∈ B ∪ C. Thus x ∈ A ∩ (B ∪ C), so that F ⊂ E. It follows that E = F.
Partitions
A separation of a nonempty set A into mutually disjoint nonempty subsets is called a partition of the set A. If
A = {a, b, c, d, e, f}
then one partition of A is
X1 = {a, d}, X2 = {b, c, f}, X3 = {e}
since
A = X1 ∪ X2 ∪ X3
with X1 = ∅, X2 = ∅, X3 = ∅, and
X1 ∩ X2 = ∅, X1 ∩ X3 = ∅, X2 ∩ X3 = ∅.
Power set
For any set A, the power set of A, denoted by P(A), is the set of all subsets of A and is written as
P(A) := {B | B ⊆ A}
so the elements of P(A) are subsets (or parts) of A. The subset of A containing only one element a is known as singleton and it is indicated by {a}, to avoid confusion with the element a ∈ A. Thus a ∈ A but a ∉ P(A). On the other hand {a} ⊆ P(A).
Note. Another notation for power set is {0, 1}A, often even using 2 instead of {0,1}, as 2A. ■
Example 1.1.2 Let A = {a, b, c}, the power set is
P(A) = {Ø, {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}}
The power set of a finite set with n elements has 2n elements because, in defining a subset, we have two independent choices for each element (does it belong to the subset or not?). In Example 1.1.2, A has 3 elements and P(A) has 23 = 8 elements.
De Morgan's Laws
The following are the statements of De Morgan’s Laws
(A ∪ B)c = Ac ∩ Bc
(A ∩ B)c = Ac ∪ Bc
The first law says that the complement of a union is the intersection of the individual complements. The second similarly says that the complement of an intersection is the union of the individual complements. (See exercise 5).
Cartesian Product
The Cartesian product is another way to create new sets from old ones. More importantly, the Cartesian product of two sets gives a rigorous model to the mental notion of pairing or ordering elements from sets.
Definition Let A and B be sets. The Cartesian product of A and B, denoted A × B is the set that consists of ordered pairs (a, b), where a ∈ A and b ∈ B. Hence,
A x B := {(a,b) | a ∈ A, b ∈ B}
More generally, if A1, A2, ..., An are n sets, then we define the Cartesian product A1, A2, ..., An as the set of ordered n-tuples (a1, a2, ..., an) with ai ∈ Ai for i = 1, 2, ..., n.
More specifically,
A x B := {(a,b) | a ∈ A, b ∈ B}
A1 x A2 x ... x An := {(a1, a2 , ..., a n) | ai ∈ Ai, for i = 1, 2, ..., n}.
For example if A = {1,5} and B = {3,2}, then
A x B = {(1,3),(1,2),(5,3),(5,2)}
whilst
B x A = {(3,1),(3,5),(2,1),(2,5)}
As can be noted by this example in general the cartesian product is not commutative, i.e. A x B ≠ B x A.
The Cartesian coordinate system motivates the concept of the Cartesian product. The notation ℝ2 stands for ordered pairs of real numbers ℝ x ℝ, which we regularly use to locate points in the Euclidean plane (in reference to a set of axes). Similarly, ℝ3 is the set of triples of real numbers and represents Euclidean 3-space.