Least common multiple

Definition 2.7.1. Let a,b ∈ ℤ. We define Least common multiple between a and b a integer m such that

m is a multiple of a and b;
if m' is a common multiple of a and b, then m' is a multiple of m as well.

The positive least common multiple between a and b is denoted by lcm(a,b).

Example. What is the lcm of 4 and 6?

Multiples of 4 are:

4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, ...

and the multiples of 6 are:

6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, ...

Common multiples of 4 and 6 are simply the numbers that are in both lists:

12, 24, 36, 48, 60, 72, ....

So, from this list of the first few common multiples of the numbers 4 and 6, their least common multiple is 12.

The fundamental theorem of arithemtic gives us a method for the calculation of the gcd and another for the calculation of the lcm of two integers (same method learned at school). The integers a and b are decomposed in primes (we know that this factorization is always possible and unique). Let

a = p₁^h₁ p₂^h₂ ... p_r^h_r, b = p₁^k₁ p₂^k₂ ... p_r^k_r

are the factorisations of a and b with p₁, ... , p_r distinct prime numbers and h₁, h₂ ... h_r^h_r, k₁, ... , k_r non-negative numbers; The number of distinct prime numbers is equal in both factorization because we admit exponents to be null. In this way "we force" into the factorization primes numbers that are not part of it. It is easy noticable that

gcd(a,b) = p₁^m₁ p₂^m₂ ... p_r^m_r

and

lcm(a,b) = p₁^M₁ p₂^M₂ ... p_r^M_r

with m_i = min {h_i, k_i}, M_i = max{h_i, k_i}. By the way this method of computation of the lcm and gcd is not very efficient. Conviene osservare che vale la seguente relazione tra gcd(a, b) and lcm(a,b):

lcm (a,b) = |a ⋅ b| / gcd(a,b)

Allora, per calcolare il minimo comune multiplo di due interi a and b, it is more conven to use the Euclidean algorith and then use the relation above.

Example the number 90 can be factorized as:

90 = 2¹ ⋅ 3² ⋅ 5¹ = 2 ⋅ 3 ⋅ 3 ⋅ 5

Here we have the composite number 90 made up of one atom of the prime number 2, two atoms of the prime number 3 and one atom of the prime number 5.

This knowledge can be used to find the LCM of a set of numbers. Example: Find the value of lcm(8,9,21).

First, factor each number and express it as a product of prime number powers.

8 = 2³

9 = 3²

21 = 3¹ ⋅ 7¹

The lcm will be the product of multiplying the highest power of each prime number together. The highest power of the three prime numbers 2, 3, and 7 is 2³, 3², and 7¹, respectively. Thus,

lcm⁡ (8 ,9, 21) = 2³ ⋅ 3² ⋅ 7¹ = 8 ⋅ 9 ⋅ 7 = 504

This method is not as efficient as reducing to the greatest common divisor, since there is no known general efficient algorithm for integer factorization, but is useful for illustrating concepts.

This method can be illustrated using a Venn diagram as follows. Find the prime factorization of each of the two numbers. Put the prime factors into a Venn diagram with one circle for each of the two numbers, and all factors they share in common in the intersection. To find the LCM, just multiply all of the prime numbers in the diagram.

Here is an example:

48 = 2 × 2 × 2 × 2 × 3,

180 = 2 × 2 × 3 × 3 × 5,

and what they share in common is two "2"s and a "3":

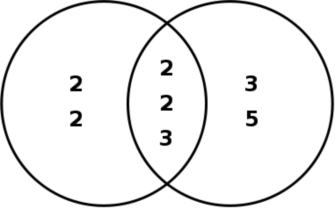
Least common multiple = 2 × 2 × 2 × 2 × 3 × 3 × 5 = 720

Greatest common divisor = 2 × 2 × 3 = 12

This also works for the greatest common divisor (GCD), except that instead of multiplying all of the numbers in the Venn diagram, one multiplies only the prime factors that are in the intersection. Thus the GCD of 48 and 180 is 2 × 2 × 3 = 12.

The fundamental theorem of arithmetic allows us to prove that the number of primes is infinite; This proof was given by the ancient Greek mathematician Euclid.

Proposition 2.7 (Euclid’s Theorem on Primes). There exist infinite prime numbers

Proof. Suppose at first that there is a finite number of prime numbers; let these p₁, p₂, p_N. Consider now the element a = p₁ ⋅ p₂ ⋅ p_N + 1. a is an integer greater than 1, thus the fundamental theorem of arithmetic guarantees us its factorization in terms of prime numbers. Nevertheless there is no prime number dividing a, since a divided by a number p_i yields as remainder 1. This is an absurd, hence prime numbers are necessarily infinite.□

« The Fundamental Theorem of Arithmetic Index Least common multiple »