Exercises on splitting fields
Consider p(x) = x2 + x + 2 over ℤ3. Let b one of its roots. Prove that ℤ3(b) is a splitting field for p(x).
Find all irreducible polynomials p(x) of second degree in ℤ2[x]. For each one of these polynomial compute the field ℤ2/(p(x)).
Prove that the polynomial f(x) = x3 + x2 + 1 is irreducible over ℤ2. Let a one of its root (which of course does not belong to ℤ2, but to ℤ2(a)), prove that ℤ2(a) is the splitting field of f(x).
Let α a root of the polynomial x2 + x + 1 ∈ ℤ5[x], irreducible over ℤ5. Calculate the extension ℤ5(α).
Check whether x2 + 1 is reducible or irreducible over ℤ3. List the elements of ℤ3(α), with α a root of x2 + 1 and write the multiplicative talbe of ℤ3(α).
Calculate the inverse of the element 3 + α in ℤ5(α), with α is a root of the polynomial x2 + x + 1 ∈ ℤ5[x].
Calculate the splitting field over ℚ of the following polynomials in ℚ[x].
x3 + 2x2 + 5x + 10
x4 −7x2 + 10
x5 + 2x4 − 5x3 − 10x2 + 6 x + 12
x3 − 1
x6 + x4 −4x2 − 4
x4 −4x2 + 2
Solutions
Z3[x]/(x2 + x + 2) ≃ ℤ3(b) = {0, 1, 2, b, 2b, b + 1, 2b + 1, b + 2, 2b + 2}. Performing long division x2 + x + 2 : (x − b)
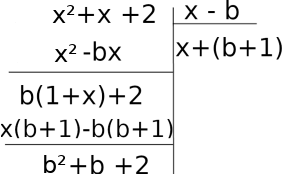
Note how the remainder of the division b2 + b + 2 = 0, in ℤ3(b). So, x2 + x + 2 = (x − b)(x + b + 1). ■
The only polynomial irreducible of 2nd degree in ℤ2[x] is x2 + x + 1. This polynomial has no roots in ℤ2 so it is irreducible. We have already calculated the field in Example 8.2.5.. ■
It is a 3rd degree polynomial without roots in ℤ2, thus it is irreducible. We calculate ℤ2[x]/(p(x)) as in the previous exercise.
ℤ2[x]/((p(x)) = {0, 1, x, x + 1, x2, x2 + x, x2 + 1, x2 + x + 1}
by theorem 8.1.16 Theorem (c) we know ℤ2[x]/((p(x)) ≃ ℤ2(α) = {0, 1, α, 1 + α, α2, 1 + α2, α + α2, 1 + α + α2| α3 + α2 + 1 = 0}.
We try to check whether the other elements of the field can be roots of p(x). First note that
(α3 + α2 + 1)2 = 0
[(α2 + 1) + α3]2 = 0
α4 + 1 + α6 = 0If we replace α2 in p(x) we get:
(α2)3 + (α2)2 = α6 + α4 + 1 = 0 (is = 0 from the relation above).
Let's check the remaining elements, say 1 + α + α2. We must compute (1 + α + α2)3 + (1 + α + α2)2 + 1:
(1 + α + α2)3 = [(1 + α) + α2]3 = (1 + α)3 + α6 + 3(1 + α)2 α2 + 3(1 + α)α4
= (1 + α)3 + α6 + α2(1 + α)2 + (1 + α)α4 = 1 + α3 + 3α2 + 3α + α6 + α2 + α4 + α4 + α5
= 1 + α3 + α + α6 + α5 = 1 + α + (α3 + α5 + α6) = 1 + α + α3(1 + α2 + α3) = 1 + α(1 + α + α2)2 = [(1 + α)2 + α2]2 = 1 + α2 + α4
Then
(1 + α + α2)3 + (1 + α + α2)2 + 1 = 1 + α + α2 + α4 + 1 + 1 = 1 + α + α4 + α2 = 1 + α + (α4 + α2) = 1 + α + α2(α2 + 1) = 1 + α + α2(α + 1)2
1 + α + α2(α + 1)2 = (1 + α)[1 + α2(1 + α)] = (1 + α)[1 + α2 + α3] = (1 + α) ⋅ 0 = 0The elements of ℤ5[x]/((p(x)) ≃ ℤ5(α) = {k + mα: α2 + α +1 =0, k,m ∈ ℤ5} are residue classes i.e. polynomials r(x) such that deg(r(x)) < deg(x2 + x + 1), are the following 25 elements
0, x, x + 1, 2x + 1, 3x + 1, 4x +1
1, 2x, x + 2, 2x+ 2, 3x + 2, 4x + 1
2, 3x, x + 3, 2x + 3, 3x + 3, 4x + 3
3, 4x, x + 4, 2x + 4, 3x + 4, 4x + 4
4By long division (x2 + x + 1): (x − α) = [x + (1 + α)], we find the 2nd root −(1 + α). Since an element of ℤ5(α) can be represented as k + ma, −(1 + α) corresponds to, by setting
k = −1 mod 5
m = −1 mod 5to 4a + 4. Which Indeed by replacing p(4α + 4) = (4α + 4)2 + 4α + 4 +1 = 16α2 + 16 + 32α = 0 since 16α2 + 16 + 32α = α2x + x + 1 mod(5). ■
It is irreducible over ℤ3 because it is a 2nd degree polynomial without roots in ℤ3. It results
ℤ3(α) = {0, 1, 2, α, 2α, 1 + α, 1 + 2α, 2 + α, 2 + 2α}
To build the multiplicative table we must take into account that α2 = −1 e.g: (α + 1)2 = α2 + 2α + 1 = −1 + 2α + 1 = 2α.
⋅ 0 1 2 α 2α 1 + α 1 + 2α 2 + α 2 + 2α 0 0 0 0 0 0 0 0 0 0 1 0 1 2 α 2α 1 + α 1 + 2α 2 + α 2 + 2α 2 0 2 1 2α α 2 + 2α 2 + α 1 + 2α 1 + α α 0 α 2α 2 1 α + 2 α + 1 2α + 2 2α + 1 2α 0 2α α 1 2 2α + 1 2α + 2 α + 1 α + 2 1 + α 0 1 + α 2 + 2α α + 2 2α + 1 2α 2 1 α 1 + 2α 0 1 + 2α 2 + α α + 1 2α + 2 2 α 2α 1 2 + α 0 2 + α 1 + 2α 2α + 2 α + 1 1 2α α 2 2 + 2α 0 2 + 2α 1 + α 2α + 1 α + 2 α 1 2 2α We are dealing with the field ℤ5(α) = {k + mα: α2 + α +1 = 0, k,m ∈ ℤ5}, so
(3 + α) (k + mα) = 1
3k + 3mα + αk + mα2 = 1we can substitute the &alpa;2 term with 4α + 4 since α2 + α + 1 = 0. Then
2mα + 3k + αk + 4m = 1
We group the terms in α and the constants
α(2m + k) + 3k + 4m = 1
Since the right-hand side of the equation does not contain terms in α we must have α(2m + k) = 0 ⟼ 2m + k = 0.
On the other hand the constant terms must be equal to 1 that is 3k + 4m = 1. By replacing k = −2m in this latter we get m = 2 and k = 1 which means the inverse element is 2α + 1. ■-
For a 3rd degree polynomial to be reducible it must possess at least a root. By the Rational root theorem, a possible root of the polynomial must be in the set {±1,±2,±5,±10}. It's easily verified −2 is a root, so we can divide the original poly by (x − (−2)) and get x2 + 5. So the possible roots are ±sqrt(5)i and the splitting field is ℚ(sqrt(5)i). ■
The polynomial could split in f(x) = g(x) ⋅ h(x) where deg(g(x)) = deg(h(x)) = 2 or could have a linear factor. In the latter case the polynomial must have a root. By the Rational root theorem the possible roots are {±1,±2,±5,±10}. Since none of those is a root we examine the first case. By the replacement x2 = y we have the polynomial
y2 −7y + 10
again the possible roots are {±1,±2,±5,±10}, and we notice that both 5 and 2 are roots then y2 −7y + 10 = (y − 5) (y − 2). Replacing back x2 we have x4 −7y2 + 10 = (x2 − 5) (x2 − 2). Thus the polynomial splits into first-degree factors in ℚ(√5,√2). ■
By the Rational root theorem the possible roots are {±1,±2,±3,±4,±6,±12} and −2 is one of them. By peforming (x5 + 2x4 − 5x3 − 10x2 + 6 x + 12):(x +2) we obtain x4−5x2 + 6. The possible roots of x4−5x2 + 6 are {±1,±2,±3,±6} and none of them is a root. By replacing x2 = y we obtain the polynomial y2 −5y + 6 having roots 3 and 2, thus y2 −5y + 6 = (y − 2) (y − 3) = (x2 −2) (x2 − 3). Thus the splitting field is ℚ(√3, √2). ■
The polynomial splits over ℚ as x3 −1 = (x − 1) (x2 + x + 1). The complex roots of x2 + x + 1 are
x = [−1 ± sqrt(1 − 4)]/2 = −1/2 ± √3i/2
So the splitting field could be written as ℚ(1, −1/2 − √3i/2 , −1/2 + √3i/2). Let ω = −1/2 + √3i/2, notice that
ω̅ =ω2 = −1/2 − √3i/2
so ℚ(1, −1/2 − √3i/2 , −1/2 + √3i/2) = ℚ(1,ω, ω2), or more simply ℚ(ω). We now describe the splitting field as vector space over ℚ: We employ Theorem 8.2.13 and use the fact that F(ω) ≃ F[x]/⟨p(x)⟩, where p(x) = x2 + x + 1, which is the irreducible polynomial in ℚ, with root ω. Since deg(p(x) = 2, then {1, ω} is a basis for ℚ(ω) over ℚ, which can be written as
ℚ(ω) = {a + bω | a,b ∈ ℚ} ■
By the rational root theorem the possible roots are {±1,±2,±4}. The fact that none of them is a root implies that the polynomial does not split in linear factors over ℚ. By using the substitution y = x2, we obtain the polynomial y3 + y2 − 4y − 4, whose roots are −1, and ±2
y3 + y2 − 4y − 4 = (y − 2) (y + 2) (y + 1).
Replacing back x we have x6 + x4 −4x2 − 4 = (x2 − 2) (x2 + 2) (x2 + 1). So the splitting field is ℚ(√2, i). ■
Make the substitution y = x2 which yields to y2 − 4y + 2, and solve this quadratic to get y = [4 ± √8]/2 = 2 ±√2. So
y2 − 4y + 2 = (y + 2 ±√2) (y − 2 ±√2)
Replacing back x we have as roots the square roots of each of the two values found i.e. ±√(2 ±√2). We can express the splitting field as ℚ(√(2 + √2)) since ℚ(√(2 +√2)) = {q0 + q1√(2 + √2) + q2 (2 + √2) + q3 (√(2 +√2))3}, and we have that 2 + √2 (and thus √2) is in ℚ(√(2 + √2)). But then
√2/√(2+√2) = √(2−√2) ∈ ℚ(√(2 + √2)). ■