Constructions with Straightedge and Compass

Let 𝒫, a set of points (finite or infinite) in the plane ℝ x ℝ. Consider the following fundamental operations

1. Draw the line between two arbitrary points of 𝒫 (ruler);

2. draw the line through arbitrary two points of 𝒫;

3. draw a circle having as center a point of 𝒫 and as radius a segment identified by two points of 𝒫.(Compass)

Definition 9.1.1 A point is said to be constructible in one step starting from 𝒫 if it is given by the intersection of any two straight lines, of a circle with a straight line, of two circles, drawn with the operations listed above.  □

A point is constructible in a finite succession of steps starting from 𝒫, if it can be obtained iterating this construction finitely many times adding to 𝒫 the points constructed in the previous steps.

Definition 9.1.2. A point P in the plane is said to be constructible in n steps from 𝒫 if there exists a finite sequence P₁, P₂, ... , P_n of points in the plane such that P_n = P and for i = 1, ... , n, P_i is constructible in one step from

A straight edge and compass constructions a finite succession of basic operations.

Examples of Classical Constructions

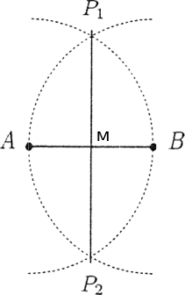
Example 9.1.3 (Construction of the midpoint of a segment). Let (AB) be a line passing through two points A and B. Draw the circles, 𝐶₁, 𝐶₂, respectively of center A and B radius the length of the segment AB. Let P₁, and P₂ the intersection points of 𝐶₁ and 𝐶₂. The mid point, M, is given by of the line (AB) with the line passing through P₁, and P₂.  ■

Example 9.1.4 (Construction of the line perpendicular to a given line, passing through a given point P which may or may not lie on the line r). Suppose first P ∉ r. The line r is given by two points P₁, and P₂. Draw the circle, 𝐶 of center P and radius the length between P and one of the two points, say P₁. If the circle 𝐶 is tangent to the line r, the line passing through P and P₁ is the perpendicular we look for. If not let P'₁ another intersection point of 𝐶 with the line r, the perpendicular is the line passing through P and the midpoint of the segment P₁P₁'.
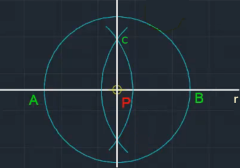
If P ∈ r, we draw a circle of a given radius around P, intersecting r at A and B. Then similarly to example 9.1.3 we draw two circles 𝐶₁, 𝐶₂, respectively of center A and B radius the length of the segment AB (see figure below). Let C the intersection between the two circles, then the line passing through C and P is the perpendicular we look for. ■

Example 9.1.5 (Given a point P external to a line L, construct the parallel line to L, passing through P). It suffices to repeat twice the construction of the perpendicular: given a line L and a point P, produces another line L' which is perpendicular to L and passes through P. Now, using this procedure again, you can construct a line L'' which is perpendicular to L' and passes through P. Since L, L' and L'' are lines on the same plane, and L and L'' are both perpendicular to L', then L and L'' must be parallel.  ■

Constructible lenghts and numbers

We want to answer the following question given a line segment in the plane, which we say is of lenght 1, for what values α can we construct a line segment of length α? To be able to deal with lenghts, we must define a unit of measure; We start by two random points, and we define the unit length as the distance between them; The unit of measurement has length = 1 by definition . We begin by observing that all the natural numbers can be constructed. In general we give the following definition:

Definition 9.1.6. A real number α is said to be constructible, if with straightedge, the unit of measurement and compass it is possible to construct a segment of length |α|. □

Thus the integers are constructible because the natural numbers are. But real numbers like π are not.

Notice that with straightedge and compass is possible to construct in ℝ x ℝ a system of Cartesian axes. It follows that a point P is constructible if and only if, its coordinates with respect to a Cartesian axes are.

We shall now prove that both ℤ and ℚ are contained in the set of numbers that can be constructed starting from only two points (the extremes of the unit of measurement); called ℭ the set of such constructible points, it is shown that ℭ is a field.

Proposition 9.1.7.

1. ℭ ⊃ ℤ;

2. ℭ ⊃ ℚ;

3. ℭ is a field.

Proof. a) Let the unit of lenght be provided by the line segment joining two points A and B. Let us rename these points as 0 and 1. The numbers 0 and 1 result constructible by definition. We can construct the number 2 by placing the point of out compass at 1 and draw the circle with radius from 1 to 0. Then clearly 3 can be constructed by placing the compass with radius 1 so as to make a circle centeres at 2, and similarly all the natural numbers can be constructed.
b) It suffices to show that every number of the form 1/n is constructible. To this end we employ Thales' theorem.

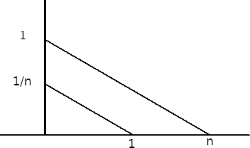
Every rational number is also sum of fraction of the form 1/n, which are constructible.

c) To prove ℭ is a field, it sufficies to show that given α and β ∈ ℭ, then α ± β, α ⋅ β and α / β with β ≠ 0. are constructible. Regarding α ± β the construction is obviuos. The figure below show how to construct αβ and α/β based on Thales theorem.

We thus proved that the set of constructible numbers is a subfield of ℝ, which contains the rational numbers.  □

We shall now give an algebraic characterization of the elements of ℭ. Let F an arbritary field of ℝ.

Definition 9.1.8. We define plane of F the subset F x F of ℝ x ℝ. We define line of F a line connecting two points in the plane of F. We define circle of F, a circle with center in the plane of F and ray equal to the lenght of a number of F.  □

We can easily verify that lines and circle of F have the following form:

Starting from the points of 𝒫 in the plane of F, which new points of the real plane can be obtained by Euclidean construction? We can obtain points by

• Intersection of two lines of F: in this however we do not obtain new points, since two lines intersecting in the plane of F, intersect in a point with coordinate in F.

• Intersection of a line and a circle of F;

• Intersection of two circles of F: as in the second case.

In the second case, the point of intersection has coordinates whch are solutions of a quadratic equation, hence belonging to either F or a quadratic extension of F, F(√a), a ∈ F. The only points of the real plane which are constructible starting from the the plane F are those points whose coordinates are in fields of the form F(α), α ∈ ℝ, α² ∈ F. Every point with coordinates in F is constructible, consider indeed the following method offers a way to construct the square root, of a constructible number a: draw the circle of radius 1 + a. Draw the perpendicular to the point 1 and let P the point of intersectrion of this perpendicular with the center, the lenght x of a segment {1, P} is the square root we were looking for: for the Euclid's theorem, x² = a.

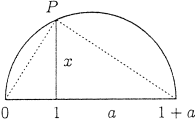
Thus all and the only points of the real plane constructible in a step starting from the plane of F are the points of coordinates in field of the form F(α), with α ∈ ℝ, α² ∈ F. The points of the real plane constructible in a step starting from the plane of F₁ are all form F₁(α), with β ∈ ℝ, β² ∈ F₁. Iterating the method this way, we see that a point c of the real plane is constructible starting from the plane of a field F if and only if and only if there exists a finite sequence of subfields:

such that ∀i = 1,...,n

with c having coordinates in F_n. Since we know that all constructible numbers contain the field ℚ, we thus proved the following algebraic characterization of real points (or number) which are constructible:

Definition 9.1.9. A real number c is constructible if and only if there exists a finite number of real numbers such that α₁, α₂, ..., α_n, such that

such that

We can calculate the degree of the extension ℚ(α₁, α₂, ..., α_n) in which c is contained as

Every factor in the right side has either degree 1 or 2, thus

for a given h ∈ ℕ. We sum up this result in the following proposition

Proposition 9.1.10. If a real number satisfies an irreducible polynomial of degree n which is not a power of two, then it is not constructible.

Proof. If α satisfies an irreducible polynomial with degree n, we know that this is the minimal polynomial; thus the extension [ℚ(α) : ℚ] = n ≠ 2^h, and α cannot belong to an extension with degree a power of 2, as it would be in the case of α constructible.  □

The ancient Greeks were interested in the geometry that is constructible using only. We shall prove now that certain constructions are impossible.

9.1.11 Doubling the cube. Can one construct a cube having double the volume of a given cube? Given a cube of unitary volume V to construct a cube of volume 2, we must construct a segment of length ∛2. If we let α = ∛2, the number α saisfies the irreducible polynomial over ℚ: x³ − 2. Since the degree of this polynomial is not a a power of 2, by proprosition 9.1.10 it cannot be constructed.  □

9.1.12 Squaring the circle. Another classical construction problem is that of squaring the circle, the problem of constructing a square whose area is the same as the ara of a given circle with a given radius. Since the unit circle has area π, this amounts to constructing the number √π, which would be the side length of a square of that same area. But Ferdinand von Lindemann proved in 1882 that π is transcendental, and so also √π is not algebraic, and therefore not constructible by straightedge and compass. So it is impossible to square the circle with those means onnly. The transcendence of π implies also that the converse problem of circling the square, to construct a circle whose area is the same as that of a given square, is impossible by straightedge and compass, since a unit square has area 1 and the circle of this area would have radius 1/√π, which is not algebraic because π is transcendental.  □

9.1.13 Rectification of the circle. The term rectification is often used to refer to the determination of the length of a curve. Given a circle with unitary radius the problem is that of drawing a segment having length 2π. Since 2π is trascendental this construction is not possible.  □

9.1.14 Trisecting Angles. Consider the trisection of angles by ruler and compass. We can easily trisect a 90° angle. Simply construct an equilateral triangle and then bisect one of its 60° angles. However there is no general ruler and compass method for trisecting all angles. It suffices to consider the angle 3θ = π/3, and try trisect it to have θ = π/9. It is the same thing as constructing cos θ. From the well-known trigonometric relation.

which for 3θ = π/3,

Thus cos(π/9) satisfies the polynomial (irreducible over ℚ, see exercise 1)

with degree not a power of two. Thus cos π/9 is not constructible and π/3 cannot be trisected.
By the same method we can show now that π/2 can be trisected. From eq. 9.1.1 it results

which yields that cos π/6 satisfies the polynomial 4x³ −3x, which is not irreducible; the minimal polynomial of cos π/6 is the second degree polynomial 4x² − 3. The number cos π/6 is thus contained in a quadratic extension of ℚ and hence constructible: indeed it results that cos π/6 = √3/2, which we know to be constructible.  □

Nota Bene. If an element satisfies an irreducible polynomial having as degree a power of two, we cannot conclude that the element is constructible. In the example above related to the construction of cos π/6, we concluded its constructibility since the degree was exactly 2. ■

Exercises

1. Prove that with ruler and compass is possible to construct a system of cartesian axes.

2. Prove that α and β are two transcendental numbers then either α + β or αβ is transcendental

Solutions

2. By Theorem 8.2.22 we known that the roots of a polynomial with algebraic coefficients, are algebraic. If both α and β were algebraic then α and β would be roots of the polynomial

   x² − (α + β)x + αβ

   having algebraic coefficients, thus α and β would be algebraic.  ■