Maxwell relations
We have defined all independent energy quantities in terms of P, V, T, and S, we summarize them in terms of their natural variables:
dU = T dS − PdV
dH = T dS + V dP
dA = −S dT − PdV
dG = −S dT + V dP
These equations are important because when the behaviors of these energies on their natural variables are known, all thermodynamic properties of the system can be determined. For example, consider the internal energy, U. Its natural variables are S and V; that is, the internal energy is a function of S and V:
U = U(S, V)
In the hyphotesis of a differentiable function z in the variables x and y, we can write
dz = (∂z/∂x)y dx + (∂z/∂y)x dy ≡ M dx + N dy
where we defined the functions M and N as:
M ≡ (∂z/∂x)y; N ≡ (∂z/∂y)x
We apply now this relation to Gibbs equations. The one for dU is
dU = TdS = PdV = M dx + N dy where M ≡ T, N ≡ P, x ≡ S, y ≡ V
Note that S and V are considered to be the independent variables of U. We therefore have the following relations
(∂U/∂S)V = T
(∂U/∂V)S = −P
The first equation states that the change in internal energy as the entropy changes at constant volume equals the temperature of the system. The second Equation shows that the change in internal energy as the volume changes at constant entropy equals the negative of the pressure. It means that we do not have to actually measure the change in internal energy versus volume at constant entropy—if we know the pressure of the system, the negative value of it equals that change.
Other relationships can be derived from the other natural variable equations. From dH:
(∂H/∂S)P = T
(∂H/∂P)S = V
From dA:
(∂A/∂T)V = −S
(∂A/∂V)T = −P
From dG:
(∂G/∂T)P = −S
(∂G/∂V)T = V
Maxwell Relations
Let us consider a continuous function f(x,y) that has continuous partial derivatives with respect to the variables x and y. The Schwarz theorem states that the order of the partial derivatives of f(x,y) can be interchanged, i.e.
∂/∂y(∂f/∂x)y = ∂/∂x(∂f/∂y)x
Applying the Schwarz theorem to the thermodynamic potentials U(S, V), A(T, V), H(S,P) and G(T,P), we obtain the Maxwell relations. Applying the Schwarz theorem to the internal energy U(S,V)
∂/∂S(∂U/∂V)S = ∂/∂V(∂U/∂S)V
Using the relations we derived before for the partial derivatived of the internal energy with respecto to volume and entropy, we obtain the Maxwell relation
−(∂P/∂S)V =
(∂T/∂V)S
For the other thermodynamic potentials we have the following relations
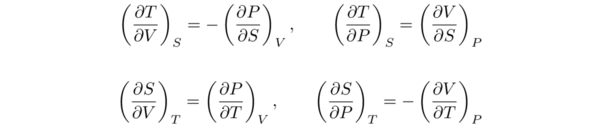
These are the Maxwell relations. The first two Maxwell relations are little used. The last two are extremely valuable, since they relate the isothermal pressure and volume variations of entropy to measurable properties.
The last equations in are examples of the powerful and remarkable relationships that thermodynamics gives us. Suppose we want to know the effect of an isothermal pressure change on the entropy of a system. We cannot check out an entropy meter to monitor S as P changes. However, the relation (∂S/∂P)T = (∂V/∂T)P tells us that all we have to do is measure the rate of change of the system’s volume with temperature at constant P, and this simple measurement enables us to calculate the rate of change of the system’s entropy with respect to pressure at constant T.