Entropy, reversibility, and irreversibility

The entropy change on going from state 1 to state 2 is given by integrating dS = dq_rev/dT from state 1 to 2 to obtain ΔS = S₂ − S₁ = ∫₁²   dq_rev/T, where T is the absolute temperature. For an irreversible process, we cannot integrate dq_irr/T to obtain ΔS because dS equals dq_rev/T only for reversible processes. For an irreversible process, dS is not necessarily equal to dq_irr/T. However, S is a state function, and therefore ΔS depends only on the initial and final states. To calculate ΔS = S₂ − S₁, we devise a reversible path from state 1 to state 2 and we use

To evaluate this integral, there are two possible scenarios. For a reversible isothermal process (including reversible phase changes), we take 1/T outside the integral. For constant-pressure heating without a phase change, we use C_P = dq_P /dT to write dq = C_P dT and then integrate (C_P /T). For a process in an ideal gas, we use the first law to write dq = dU − dw = C_V dT = P dV, substitute this into the ΔS equation, use PV = nRT to express P/T as a function of V, and integrate.

So far, we have focused on the entropy change of an isolated system and can properly label the ΔS as ΔS_sys?. What about the entropy change of nonisolated systems, and the concurrent change in the entropy of the surroundings, labeled ΔS_surr? Typically, the surroundings are much larger than the system of interest, and the temperature of the relatively large surroundings can be taken as constant. Thus, we suggest parrallel to the variation of entropy for the system the equation dS_{surr = dqsurr /Tsurr which integrates to}

Reversible Processes

In a reversible process, any heat flow between system and surroundings must occur with no finite temperature difference; otherwise the heat flow would be irreversible. Let δq_rev be the heat flow into the system from the surroundings during an infinitesimal part of the reversible process. The corresponding heat flow into the surroundings is −δq_rev. We have

Irreversible Processes

Many irreversible transformations begin with the system in one equlibrium or metastable state and end with the system in another equilibrium state. Since entropy is a state function, we can calculate ∆S for an irreversible process that is not reversible so long as it has equilibrium or metastable initial and final states by calculating on a reversible path with the same initial and final states. For the calculation of the entropy change of the surroundings a separate calculation is necessary, since the final state of the surroundings will not necessarily be the same in the reversible as in the irreversible process.

Consider an adiabatic irreversible process in a closed system. The system undergoes an irreversible adiabatic transformation from state 1 to state 2. The disconnected line segments from 1 to 2 in Fig. 1 indicate the irreversibility and the fact that an irreversible process cannot in general be plotted on a P-V diagram since it usually involves non-equilibrium states.

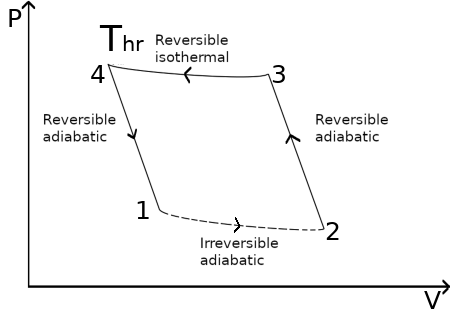
To evaluate ΔS_syst = S₂ − S₁, we connect states 1 and 2 by the following reversible path: From state 2, we do work adiabatically and reversibly on the system to increase its temperature to T_hr, the temperature of a certain heat reservoir. This brings the system to state 3. Since there is no heat exchange, ΔS is zero: the transformation is an isentrop for a reversible adiabatic process. Hence S₂ = S₃. Next we either add or withdraw enough heat q_3→4 isothermally and reversibly at temperature T_hr to make the entropy of the system equal to S₁, bringing the system to state 4 with S₄ = S₁. From state 4 to state 1 we have another isentrop. The variation of entropy for the whole reversible transformation from 2 to 1, is given only by the contribution of the reversible isothermal process from 3 to 4; We have

Since S is a state function, we have for the cycle 1 → 2 → 3 → 4 → 1

Which is the desidere entropy variation for the irreversible adiabatic process from 1 to 2.

Since U is a state function ΔU = 0 for the cycle, and the work done on the system in the cycle is thus w = −q_3→4. The work done by the system on the surroundings is −w = q_3→4. Suppose q_3→4 were positive. Then the work w done on the surroundings would be positive, and we would have a cycle (1 → 2 → 3 → 4 → 1) whose sole effect is extraction of heat q_3→4 from a reservoir and its complete conversion to work −w = q_3→4 > 0. Such a cycle is impossible, since it violates the second law. Hence q_3→4 cannot be positive: q_3→4 < 0. Hence

As requested for an irreversible adiabatic process.

We now show that an irreversible adiabatic process must lead to a higher temperature than the reversible adiabatic process starting at the same initial state (state 1). We'll prove that the cycle depicted in Fig.2a is an absurdum; it is composed by: an adiabatic irreversible expansion (1 ⟶ 2), followed by a reversible constant volume temperature rise to state 3, and then by a reversible adiabatic compression 3 ⟶ 1, completing the cycle.

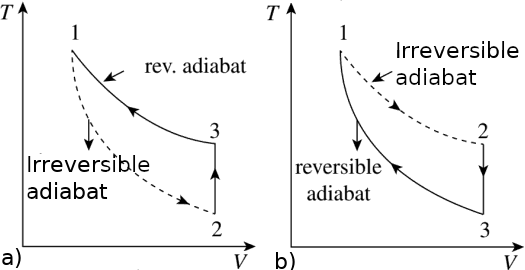
For the constant volume process in Fig.2(a), the heat absorbed by the system, during the path 2 ⟶ 3. is

The heat capacity of a system is always positive. Therefore Q₂ > 0, as the state 3 is at a higher temperature then the state 2. The cucle is then completed by a reversible adiabatic process 3 ⟶ 1. We may then write

Since U is a state function we have ΔU_cycle = 0. The net work done on the surroundings over the cycle is

This meas that the heat transferred to the system has been completely completely converted into work done on the surroundings; this is a violation of the second law. An irreversible adiabatic process cannot therefore, lead to a state that is lower in temperature than the reversible adiabat.

If state 2 is above the reversible adiabat Fig.(2b), we carry out a constant volule reversible step from state 2 to state 3, and an adiabatic reversible step from state 3 to state 1. Since state 2 is at a higher temperature than state 3, and since the heat capacity is positive

hence

In this case, heat transferred to the surroundings has been turned completely into work done on the system. This does not violate the second law of thermodynamics because the surroundings do not undergo a cyclic process.

The final temperature for an irreversible adiabatic process cannot be lower than for a reversible adiabatic process with the same final volume, but it can be higher.

Consider now the entropy change for the irreversible adiabatic process, depicted in Figure 2b. Because S is a state function,

Because step 3 is reversible and adiabatic, ∆S₃ = 0, and

Because step 2 is reversible, we can integrate and get the variation of entropy for this step:

The inequality comes from the fact that the temperature and the heat capacity are both positive and the fact that the temperature of state 2 must be greater than that of state 3. Because ∆S₁ = −∆S₂, ∆S₁ must be positive. Therefore,

For an adiabatic process we have

where the equality holds for reversible processes. For any adiabatic process, the entropy of the system cannot decrease. This is the most important consequence of the second law of thermodynamics. Because we define the universe to include all objects that interact with each other, the universe can undergo only adiabatic processes. In any reversible process, the entropy of the universe remains constant. In any irreversible process, the entropy of the universe increases.

Adiabatic Irreversible expansion

If we consider adiabatic reversible and irreversible processes, then starting from the same initial state one cannot reach the same final sate by the two paths. If the initial state of a gas corresponds to P₁,V₁,T₁ after adiabatic reversible expansion the state will correspon to P₂,V₂,T₂. For an adiabatic irreversible process, if the final volume is still V₂, the pressure and temperature will not be P₂ and T₂. They will be P_irr and T_irr. This implies that we could not go from state 1 to 2 in Fig.1 with a reversible transformation. If it is an expansion, P_irr will be greater than P₂ and T_irr will be greater than T₂. So the pressure-volume work done in the irreversible adiabatic change is not equal to dU and the relationship dU = n C_v(T₂/T₁) = −Rln(V₂/V₁) does not apply for the irreversible adiabatic change, even though δq is zero.

If the pressure exerted on the gas in now suddenly decreased from P_A to P_B, then the state of the gas is out of equilibrium and the expansion occurs irreversibly and will not follow the path PV^γ = constant.

In this case entropy is produced by the process. This change in entropy is due to internal generation of heat by fluid friction and since the gas is contained adiabatically, this heat does not leave the system and the final temperature of the gas will be higher than the temperature reached by the reversible process.

Example 1. 3 mol of an ideal monoatomic gas γ = 1.67 at 300 K and 10.19 ⋅ 10⁵ Nm^-2 is allowed to expand to 1.019 ⋅ 10⁵ Nm^-2 by, (a) a reversible adiabatic process and, (b) an irreversible adiabatic process. Calculate in each case the final temperature, final volume, w, q, ΔU and ΔH (C_p,m = 20.79 JK^-1 mol^-1 and C_V,m = 13.47 JKmol^-1).

Solution. a) Here q = 0, hence ΔU = w = nC_V(T₂ - T₁); By using eq (2.4)

The ideal gas law can be used to calculate the final volume

P₁V₁/T₁ = P₂V₂/T₂

V₂ = 119.1/300 ⋅ 10/1 ⋅ 4.9424 ⋅ 10^-3 = 19.55 ⋅ 10^-3m³

b) (Adiabatic irreversible expansion) The final temperature will be higher than that of the reversible process. The final temperature can ebe calculated from eqn (2.5)

The variation of internal energy

The final volume can be calculated using the equation of state of the perfect gas as before

«Second law of thermodynamics

Index Entropy Changes of Isothermal Processes »