Triple Product Rule
The triple product rule, known variously as the cyclic chain rule, cyclic relation, or Euler's chain rule, is a formula which relates partial derivatives of three interdependent variables. The rule finds application in thermodynamics, where frequently three variables can be related by a function of the form F(x, y, z) = 0, so each variable is given as an implicit function of the others.
Proposition 1.3 - Let (x0,y0,z0) ∈ ℝ3 and suppose F: A → ℝ, with A open subset of ℝ3 and F ∈ C1(A). Assuiming at the point (x0,y0,z0), none of the partial derivatives vanishes and F(x0,y0,z0) = 0, the foolowing identity holds:

Proof. By the implicit function theorem we may write
x = f(y,z), y = g(x,z), z = ξ(x,y)
which are are continuously differentiable at least in a small neighborhood of (x0,y0,z0).
By the mean value theorem of several variables,
(∂z/∂x)y = −Fx / Fz (3.6)
In fact applying the mean value theorem to F,
F(x + h, y, z + k) − F(x,y,z) = h ⋅ Fx(x + ϕh, y ,z) + k ⋅ Fz(x, y, z + θk), h,k ∈ℝ and θ, ϕ ∈ [0, 1]
Within a sufficiently small neighborhood of (x0,y0,z0) it results that
F(x + h,y , z + k) = F(x, y ,z) = 0
thus
Fx(x + ϕh, y, z) / Fz(x, y, z + θk) = − k / h
By the implicit function theorem z = ξ(x, y); setting k = ξ(x+h, y) − ξ(x, y) and considering the incremental ratio of z : [ξ(x+h, y) − ξ(x, y)] / h; if we now let h → 0, we get ∂z/∂x
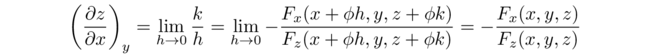
By applying the same reasoning with regards to the other functions x = f(y,z) and y = g(x,z), the following relations are obtained
(∂x/∂y)z = −Fy / Fx (3.7)
and
(∂y/∂z)x = −Fz / Fy (3.8)
Multiplying eqns (3.6), (3.7) and (3.8), we get
 □
□