Double integrals

The notion of the integral can be extended to higher dimensions. First let’s recall the basic facts concerning definite integrals of functions of a single variable. If f: [a,b] ⟶ ℝ, is a continuos function the integral is defined as

$${\int }_a^{b}f(x)\text{d}x=\underset{n\to \mathrm{\infty }}{lim}\sum _{k=1}^n\frac{b-a}{n}f(t_k)$$

where we start by dividing the interval [a,b] into n subintervals [x_k−1, x_k] of equal width (b − a)/n and we choose sample points t_k in these subintervals x_k−1 ≤ t_k ≤ x_k. In the special case where f ≥ 0 , the Riemann sum can be interpreted as the sum of the areas of the approximating rectangles, and the definite integral represents the area under the curve y = f(x) from a to b .

In a similar manner we consider a function f of two variables defined on a closed rectangle

The first step is to divide the rectangle R into subrectangles. We accomplish this by dividing the interval [a,b] into n subintervals [x_h−1, x_h] of equal width (b − a)/n and dividing [c,d] into n subintervals [y_k−1, y_k] of equal width (d − c)/n . By drawing lines parallel to the coordinate axes through the endpoints of these subintervals, froming the subrectangles

We set

$$\int {\int }_{[a,b]\times [c,d]}f(x,y)\text{d}x\text{d}y=\underset{n\to \mathrm{\infty }}{lim}\sum _{h,k=1}^n|R_{hk}|f(t_{hk})\text{\hspace{1em}4.1.1}$$

where we've chosen a sample point t_h,k in each R_hk.

Theorem 4.1.1 If f: [a,b] x [c,d] ⟶ ℝ is continuos, the limit 4.1.1 exists and it is called the double integral of f over the rectangle [a,b] x [c,d].  □

Iterated Integrals

As in the case for single variable definite integrals it is usually difficult to evaluate the integral directly from the definition of an integral, but the Fundamental Theorem of Calculus provides a much easier method. The evaluation of double integrals from the definition is even more difficult, but in this section we see how to express a double integral as an iterated integral, which can then be evaluated by calculating two single integrals.

The existence of the double integral ∫∫_D f(x,y) dA depends on f and the domain D. The evaluation of double integrals is easiest when the domain of integration is of simple type, according to the following definitions.

Definition 4.1.2 A set D of ℝ² is said to be y-simple, when it is defined as

with g₁,g₂: [a,b] ⟶ ℝ continuos functions. This means that when a line perpendicular to the x-axis runs through the set D, we obtain always a segment of width wich varies continuosly varying the line.

Analogously a set D is said x-simple

with h₁,h₂: [a,b] ⟶ ℝ continuos functions.
A domanin D is said to be simple domain if it is simple in both x and y directions. It is said regular if it is union of a finite number of simple domains.

 □

Note that if a domain D is simple (or regular) is also bounded.

Example 4.1.3. The set

is by definition y-simple, but not x-simple indeed by passing a line parallel to x we see that we don't always obtain a set representing a segment.

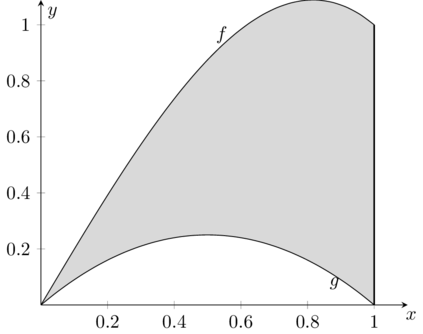
Example 4.1.4. The set represented in the following figure

is both x-simple and y-simple. It can be represented as y-simple as

or as x-simple as

To be able to calculate a double integral let consider first the geometrical interpretation; When f is a positive function, then the double integral can be interpreted as the volume of the three-dimensional region V between the surface of f(x,y) and the the plane xy-plane. Let D a x-simple domain. Consider the cross-section of this solid in the vertical plane parallel to the x-axis. The area of the cross-section if A(y). The double integral ∫∫_D f(x,y) dxdy is obtained by summing the volume of "thin" slices of area A(y) and thickness dy between y = c and y = d.

The total sum is nothing more than

$$V={\int }_c^{d}A(y)\text{d}y$$

The area of a cross section is given by means of a one-dimensional integrations of the function f(⋅,y)

$$A(y)={\int }_{a(y)}^{b(y)}f(x,y)\text{d}x$$

from which follows that

$$V={\int }_c^d({\int }_{a(y)}^{b(y)}f(x,y)\text{d}x)\text{d}y$$

This expression is called iterated integral. A theorem which asserts the equality of a double integral and an iterated integral is often referred to as a “Fubini Theorem”, after the Italian mathematician Guido Fubini (1879–1943).

Theorem 4.1.5 (Fubini’s Theorem) If f ∈ C(D) in the x-simple domain D = {(x,y) ∈ ℝ² : y ∈ [c,d], h₁(y) ≤ x ≤ h₂(y)} . Then f is integrable on D and its double integral can be calculated as iterated integrals as follows

$${\iint }_{D}f(x,y)\text{d}x\text{d}y={\int }_c^d({\int }_{h_1(y)}^{h_2(y)}f(x,y)\text{d}x)\text{d}y$$

If D is a y-simple domain then it can be calculated as

$${\iint }_{D}f(x,y)\text{d}x\text{d}y={\int }_a^b({\int }_{g_1(x)}^{g_2(x)}f(x,y)\text{d}y)\text{d}x$$

In the case of D simple domain both formulas hold and lead to the same result. □

Iteration is the process of reducing the problem of evaluating a double integral to one of evaluating two successive single definite integrals.

If D is a domain union of a finite number of simple domains (i.e. regular), intersecting at their borders, it results

$${\iint }_{D}f(x,y)\text{d}x\text{d}y=\sum _{k=1}^n{\iint }_{D_k}f(x,y)\text{d}x\text{d}y$$

Where each integral on the right-hand side can be calculated as iterated integral.

Example 4.1.6. Evaluate the integral

Where D is the simple domain depicted in Fig. 2

We can first integrate with respect to y from 0 to x/2, treating x as a constant, and then with respect to x from 0 to 2:

$${\int }_0^2\left({\int }_0^{x/2}xy\text{d}y\right)\text{d}x={\int }_0^2{\left[\frac{1}{2}x{y}^2\right]}_0^{x/2}\text{d}x={\int }_0^2\frac{x^3}{8}\text{d}x={\left[\frac{1}{32}{x}^4\right]}_0^2=\frac{1}{2}$$

Since the domain is simple we can also integrate with respect to x from 2y to 2, treating y as a constant, and then with respect to y from 0 to 1:

$${\int }_0^1\left({\int }_{2y}^{2}xy\text{d}x\right)\text{d}y={\int }_0^1{\left[\frac{1}{2}x{y}^2\right]}_{2y}^2\text{d}y={\int }_0^1(2y-2y^3)\text{d}y={[y^2-\frac{1}{2}{y}^4]}_0^1=\frac{1}{2}$$

. ■

As in the one-dimensional case it is the Riemann integral permits a precise definition of the geometrical concept of "area" under a curve and not viceversa. The area of a simple domain is defined as

Properties of double integrals

We can state analogous properties holding for the one-dimensional case

.

Theorem 4.1.6. Let D ⊂ ℝ². a regular set and let f, g continuous on D. Then

1. (Linearity) ∫∫_D [f(x,y) + g(x,y)] dxdy = ∫∫_D f(x,y) dxdy = ∫∫_D g(x,y) dxdy

   Let c a contant. Then

   ∫∫_D cf(x,y) dxdy = c ∫∫_D f(x,y)

2. (Monotonicity)

   f ≥ g in D   ⟶   ∫∫_D f(x,y) dxdy ≥ ∫∫_D g(x,y)

   in particular

   f ≥ 0 in D   ⟶   ∫∫_D f(x,y) dxdy ≥ 0

3. (Additivity of domains) Let D = D₁ ∪ D₂, with D₁ ∩ D₂ of zero measure. If f is integrable on D₁ and on D₂, then f is integrable on D, and

   ∫∫_{D1 ∪ D2} f(x,y) dxdy = ∫∫_D1 f(x,y) dxdy + ∫∫_D2 f(x,y) dxdy

4. (Mean Value Theorem) If m ≤ f(x,y) ≤ M, then

   m ⋅ area(D) ≤ ∫∫_D f(x,y) dxdy ≤ M ⋅ area(D)

   The number (x₀, y₀) ∈ D such that

   f(x₀, y₀)⋅ area(D) = ∫∫_Df(x,y) dxdy  4.1.2

   is called (integral) mean value of f on D. It can be proved that if f is continuous on D and if D is connected (i.e. D is not union of disjoint closed sets), then there exists at least a point (x₀, y₀) ∈ D such that 4.1.2 is verified. □

Example 4.1.6. Evaluate the integral

Where D is the simple domain depicted in Fig. 3

Consequently, the integral splits in the sum of two integrals, and each one can be calculated as iterated integral.

$$I={\int }_0^1\left({\int }_{x/3-1}^{x-1}xy\text{d}y\right)\text{d}x+{\int }_1^3\left({\int }_{x/3-1}^{\sqrt{1-(x-2{)}^2}}xy\text{d}y\right)\text{d}x={\int }_0^{1}x{\left[\frac{y^2}{2}\right]}_{x/3-1}^{x-1}\text{d}x+{\int }_0^{1}x{\left[\frac{y^2}{2}\right]}_{x/3-1}^{\sqrt{1-(x-2{)}^2}}\text{d}x={\int }_0^1(\frac{4}{9}{x}^3-\frac{2}{3}{x}^2)\text{d}x+{\int }_1^3(\frac{-5}{9}{x}^3+\frac{7}{3}{x}^3-2x)\text{d}x$$

which after some calculation gives −1/9 + 10/9 = 1.  ■

Observation 4.1.7. In the case where the integrand can be factored as a product of a function f(x) of x only and a function g(y) of y only, then over a rectangulare region R = {(x,y) | a ≤ x ≤ b, c ≤ y ≤ d}, the double integral can be written as

$${\iint }_{[a,b]\times [c,d]}f(x)g(y)\text{d}x\text{d}y={\int }_a^b({\int }_c^{d}f(x)g(y)\text{d}y)\text{d}x={\int }_a^{b}f(x)({\int }_c^{d}g(y)\text{d}y)\text{d}x=({\int }_c^{d}g(y)\text{d}y)({\int }_a^{b}f(x)\text{d}x)$$

«Epoxides Index Exercises on double integrals»