Rango di una matrice
Abbiamo visto che se le righe (o colonne) di A sono vettori linearmente dipendenti allora det A = 0. Per n =2 o n=3 abbiamo dimostrato anche il viceversa: il determinante si annulla se e solo se le righe della matrice sono linearmente dipendenti. Questo risultato si può generalizzare per n qualsiasi
Data una matrice A (m x n) il sottospazio ℝn generato dai vettori riga a1, a2, ..., am di A è detto spazio delle righe ed il sottospazio ℝm generato dai vettori colonna a1, a2, ..., an è detto spazio delle colonne. Tali spazi vengono indicati con ℛA e ℭA, rispettivamente. Vale il seguente teorema:
Teorema R.0 - Siano a1, a2, ...,an, r vettori riga di ℝn ( r < n) e sia A la matrice (r,n) che ha per righe questi vettori. Allora i vettori a1, a2, ...,an sono linearmente dipendenti se e solo se ogni matrice (r,r) estratta da A ha determinante nullo; sono indipendenti se e solo se esiste almeno una matrice (r,r) estratta da A, con determinante diverso da zero.
Inoltre: n vettori di ℝn sono linearmente dipendenti (indipendenti) se e solo se la matrice (n,n) che si ottiene accostandoli ha determinante uguale a zero (diverso da zero).
Teorema R.1 Lo spazio delle righe e lo spazio delle colonne di una matrice A(m,n) hanno la stessa dimensione.
Dim. Se A è la matrice nulla, sia le righe che le colonne di A sono vettori nulli. Si ha quindi dim ℛA = dim ℭA = 0. Se A non è la matrice nulla, vi è qualche vettore riga e qualche vettore colonna che non sono vettori nulli.
Per il teorema di esistenza della base, di uno spazio vettoriale, tra gli m vettori riga ci saranno al più r ≤ m vettori riga che sono una base di ℛA ed al più c ≤ n vettori colonna che sono una base di ℭA.
Senza ledere di generalità, supponiamo che {a1, a2, ..., ar} sia una base di ℛA. Allora per qualche vettore riga, ai di A si ha:
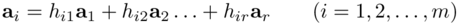
ossia in modo più esplicito come:
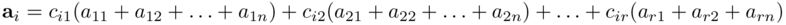
Ricavando dalla precedente il j-esimo elemento di ai, si ha:
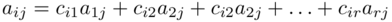
che porta alle seguenti equazioni:
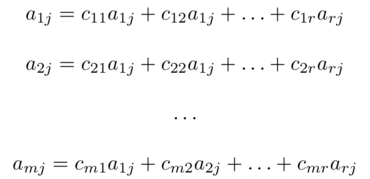
per j= 1,2, ...,n. Quest'ultima relazione mostra che il j-esimo vettore colonna aj di A, è combinazione lineare degli r vettori di ℝm.
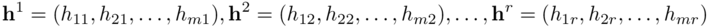
si ha quindi per j= 1,2, ...,n :
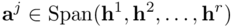
Segue quindi che ℭA⊆ Span(h1, h2, ..., hr), quindi
dim ℭA ≤ dim Span(h1, h2, ..., hr).
Ovvero:
s ≤ r.
Scambiando il ruolo delle righe e delle colonne e procededo analogamente, risulta che:
r ≤ s.
quindi:
r = s.
Essendo r ed s il numero dei vettori di una base di ℛA e ℭA rispettivamente, allora dim ℛA =dim ℭA, da cui la tesi.□
Dal teorema segue che:
Def. R.1. Dicesi rango (o caratteristica) di una matrice A(m, n), e lo si indica con r(A), il massimo numero di righe o di colonne linearmente indipendenti.
E' evidente in base al teorma R1 che:
r(A) = r(AT)