Geometric Vectors

Quantities such as force and velocity involve both magnitude and direction and cannot be completely characterized by a signle number; such quantities are called vectors.
A convenient geometrical representation of a vector is provided by a straight line segment drawn in space parallel to the required direction, with an arrowhead indicating the sense. The given lenght of the line segment represents the magnitude of the vector v, insicated by |v|.
The direction of the vector is specified by the direction cosines of a (directed) line which are the cosines of the angles which the line makes with the positive directions of the coordinate axes.

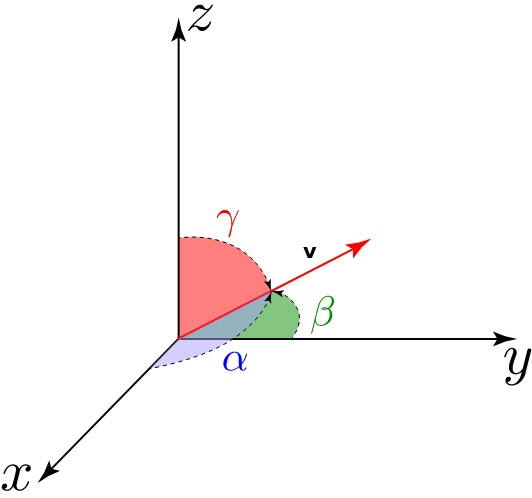
This four quantities are not independent. We know that we can calculate the length of v using Pythagoras' theorem

A vector v can be interpreted as the displacement from a point P₁ of cartesian coordinates x₁, y₁, z₁ to a specific point P₂, of cartesian coordinates x₂, y₂, z₂. The magnitude |v| of the vector is given by the Pythagoras' theorem as

$$|v|=\sqrt{(x_2-x_1{)}^2+(y_2-y_1{)}^2+(z_2-z_1{)}^2}$$

and its director cosines are

Component Form of a Vector

We have seen that the vector is characterized by dependent quantities. We want now to characterize a given vector v in terms of independent quantities, known as components of the vector. Each component is obtained by multiplying the magnitude of the vector by the direction cosine. The component form of a vector is written as v = (a,b,c), which each component expressed as

Thus a component of a vector is the projection of the vector on an axis. So a is the component along the x axis. Since the magnitude |v|, is always positive, a component will be positive or negative depending on the angle θ either acute, or obtuse. Then by 1.2.1 we find the condition

Once |v| is determined 1.2.2 give us the directors cosines so that the direction of v is fully characterized.

A vector whose magnitude is unity is called a unit vector. Given any vector v = ai + bj + ck, the unit vector having the same direction as that of given vector v is

$$\hat{\mathbf{v}}=\frac{a\mathbf{i}+b\mathbf{j}+c\mathbf{k}}{\sqrt{a^2+b^2+c^2}}$$

The coefficients $\frac{a}{\sqrt{a^2+b^2+c^2}}$ are sometimes referred to as the direction cosines (or directional cosines), they are the components (α, β, γ) of the unit vector.

Vector operations

Multiplying a vector by a scalar: If we multiply a vector v by a scalar λ, we get a new vector whose magnitude is the product of |v| by the absolute value of λ. Its direction is the direction of v is λ is positive but the opposite direction if λ is negative. In particular the symbol −v represent the vector with opposite sense as v.

Addition (sum) of two vectors: Adding two vectors, say u and v, will make a third vector w, we write

Components can also be used to find the resultant of vectors if u = (u₁, u₂, u₃) and v = (v₁, v₂, v₃) then the resulting vector is

Parallelogram Rule for Vector Additiob. If u and v are vectors that are positioned so that their initial points coincide, then the two vectors form adjacent sides of a parallelogram, and the sum u + v = w is the vector represented by the arrow from the common point of u and v to the opposite vertex of the parallelogram

Triangle Rule for Vector Addition. If u and v are vectors that are positioned so the initial point of v is at the terminal point of u, then the sum u + v is represented by the arrow from the initial point of u to the terminal point of v.

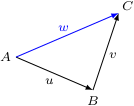
Si verifica immediatamente che la somma di vettori gode della proprietà commutativa, cioè u + v = v + u, come si può vedere nella figura seguente

Un altro metodo è quello del parallelogramma, volendo sommare due vettori a e b, si disegna un parallelogramma costituito dai lati a e b; il vettore somma a+b sarà dato dalla diagonale del parallelogramma.

The vector whose initial and terminal points coincide has length zero, so we call this the zero vector and denote it by 0. The zero vector has no natural direction, so we will agree that it can be assigned any direction that is convenient for the problem at hand.

The vector addition has the following properties: For v, w, u ∈ ℝⁿ,

1. v + w = w + v,

2. v + (w + u) = (v + w) + u,

3. there exists a zero vector 0, with the property that v + 0 = v

4. every vector v has an additive inverse −v, with the property that v + (−v) = 0.

You should recognize these as the same defining properties possessed by addition in a ring (see Chapter 6) or the properties of the operation in an abelian group (see Chapter 19). Here, the additive identity is the zero vector 0. In R³ , 0 = (0, 0, 0) and if v = (v₁, v₂, v₃), then −v = (v₁, v₂, v₃). The other arithmetic operation in the algebra of vectors is scalar multiplication, in which vectors are multiplied by scalars to give other vectors. Here, our scalars come from the field R. Scalar multiplication has the following properties: For r, s ∈ R and v, w ∈ Rⁿ,

1. (r + s)v = rv + sv,

2. (rs)v = r(sv),

3. r(v + w) = rv + rw,

4. 1v = v.

Note that the 1 in the last property is the scalar 1.

Oltre alle grandezze indicate da un numero come la tempratura il tempo il volume, etc., dette scalari, esistono grandezze fisiche che sono completamente definite solo quando sono specificati sia una magnitudine (o modulo) che una direzione ed un verso. Esempi sono la velocità, l'accelerazione e le forze. Queste che sono esempi di grandezze vettoriali.

Un vettore è un ente individuato assegnando:

1. un numero reale positivo che esprime la sua lunghezza o modulo.

2. una direazione, individuata da una retta (rette parallele individuano la stessa direzione).

3. un verso

Geometricamente, si può rappresentare un vettore come una freccia orientata. Due vettori che si sovrappongono per traslazione nello spazio (senza venire ruotati) rappresentano lo stesso vettore. Fissando nello spazio un sistema di coordinte cartesiane di cui O è l'origine, possiamo rappresentare i vettori come frecce uscenti da O:

La direzione ed il verso del vettore sono quelli indicati dalla freccia, mentre il suo modulo è la lunghezza della freccia. Un vettore è rappresentato in tal caso come un punto del piano cartesiano determinato da una coppia di numeri reali ((x , y), note come componenti scalari del vettore. Nello spazio tridimensionale un vettore è analogamente una terna di numeri reali ( x , y, z ) Si indica un vettore col simbolo , con A la punta della freccia, oppure con simboli in grassetto come v, a. Il modulo di un vettore v è indicato con |v|.

The Triangle Inequality

Proposition (Triangle inequality). Suppose that v and w are two n-dimensional vectors. Then,

The triangle inequality states that the magnitude of a sum is always less than or equal to the sum of the magnitudes of the individual vectors in the sum. Next Figures contains a geometric proof of the triangle inequality in ℝ²: Since the shortest distance between two points is a straight line, any side of any triangle is always shorter that then sum of the lenghts of the other two sides. The only case in which the rule is an equality, that is ||v + w|| = ||v|| + ||w||, is when v and w have the same direction. In this case, the triangle "collapses", and has no interior.

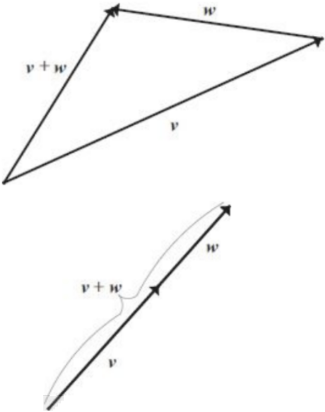
Questa figura illustra la cosiddetta regola del parallelogramma: il vettore w = u + v è la diagonale del parallelogramma che ha come lati i vettori u e v.

Subtracting Vectors

Vector subtraction makes use of the definition of the negative of a vector. We define u − v to be u + (−v). Thus vector subtraction is really a special case of vector addition. The geometric construction for subtracting two vectors is shown in the following figure.

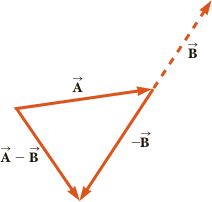
Vectors in a Cartesian (Analytic) Plane R²

Se fissiamo un sistema di coordinate cartesiane ortogonali OXY nel piano, ogni vettore v può essere rappresentato da una coppia di numeri reali (v_x, v_y), che individuano le proiezioni di v sugli assi coordinati. Possiamo quindi identificare il vettore v con la coppia (v_x, v_y) ∈ R². In termini di questa identificazione, la somma dei due vettori u = (u_x, u_y) e v = (v_x, v_y) è data da

mentre il prodotto di un numero reale λ per il vettore v = (v_x, v_y) è dato da

Usando queste formule è ora immediato verificare che la somma di vettori gode delle proprietà associativa e commutativa. Esiste poi un elemento neutro per la somma, il vettore nullo, le cui componenti sono tutte nulle, e che indicheremo con 0 = (0, 0). Inoltre, per ogni vettore v = (v_x, v_y) esiste il suo opposto −v = (−v_x, −v_y), tale che v + (−v) = 0.
Tutto ciò si può riassumere dicendo che l’insieme dei vettori, con l’operazione di somma, forma un gruppo abeliano.

«Normal subgroups Index Vector Spaces »