Divisibility of polynomials

The divisibility properties and definitions relating to integers extend to polynomials.

Proposition 5.2.1. (Algorithm for the division). Let f(x) and g(x) ∈ 𝕂[x] two polynomials with g(x) ≠ 0. Then there exist and are uniquely determined two polynomials q(x) and r(x) ∈ 𝕂[x] such that

f(x) = g(x) · q(x) + r(x), with ∂r(x) < ∂g(x) or r(x) = 0.

Proof. If f(x) = 0 or ∂r(x) < ∂g(x) is enough to set q(x) = 0 and r(x) = f(x). So suppose ∂g(x) ≤ ∂f(x). We proceed by induction on n=∂f. If n = 0 (hence also ∂g(x) = 0), we have f(x) = a₀ and g(x) = b₀, with a₀, b₀ ∈ 𝕂, thus

f(x) = a₀ = (a₀⋅b₀⁻¹) b₀ + 0

in this case r(x) = 0 and q(x) = a₀⋅b₀⁻¹.

We suppose the theorem true for polynomials of degree < n and prove it for ∂f = n. Then ∂f = n ≥ ∂g = m. Let

f(x) = a₀ + a₁ x + ··· + a_n xⁿ, g(x) = b₀ + b₁ x + ··· + b_m x^m,

we put

h(x) = f(x) − a_n b_m⁻¹ x^n−m g(x)

The degree of h(x) is smaller than n, so we may apply to h(x) the induction hypothesis. So there exist q₁>(x), r₁(x) such that

h(x) = q₁(x) g(x) + r₁(x), r₁(x) < m or ∂r₁(x) = 0.

Then

f(x) − a_n b_m⁻¹ x^n−m g(x) = h(x) = g(x) q₁ + r₁(x)

And it is enough to take r(x) = r₁(x) and q(x) = q₁(x) + (a_n b_m⁻¹)x^n−m.

As to the uniqueness of division, notice that if f(x) = g(x) · q₁ (x) + r₁ (x) = g(x) · q₂(x) + r₂ (x) such that ∂r_i(x) < ∂g(x) or r_i(x) = 0 with i = 1, 2, then we would get

g(x)(q₁(x) − q₂(x)) = (r₂(x) − r₁(x))

If it is the case that q₁ > (x) − q₂(x) ≠ 0, the left-hand side would have a greater degree than the second one, which is not possible. So we must have q₁(x) = q₂ (x), which also implies r₂(x) = r₁(x).□

Definition 5.2.2. We say that a polynomial g(x) divides a polynomial f(x) with f,g ∈ 𝕂[x] and we write g(x)| f(x) if there exists a polynomnial q(x) ∈ 𝕂[x] such that

f(x) = g(x) · q(x)

Definition 5.2.3. An element f(x) ∈ 𝕂[x] is said invertible if there exists a polynomial g(x) ∈ 𝕂[x] such that f(x)g(x) = 1.

A polynomial g(x) of degree 1 or higher, in F[x], can never be invertible, because if it had an inverse h(x), then h(x) != 0 so the product g(x) h(x) has degree deg(g) + deg(h) ≥ 1, so this product can't be 1.

Example 5.2.4. Long division of x³ − 8 by x − 2 yields

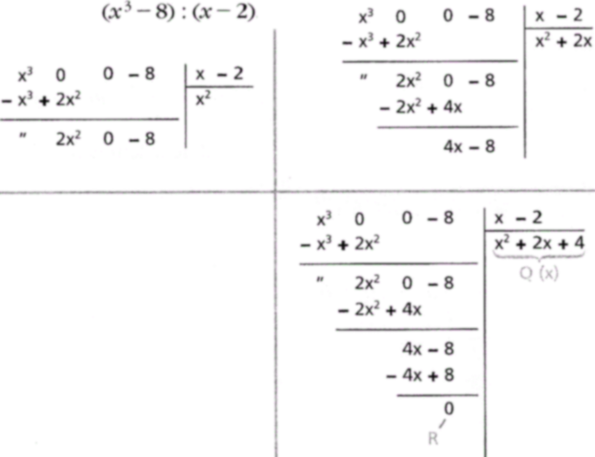
Example 5.2.5. The division of x² + x + 2 by x − b, with b a constant, leaves a remainder b² + b + 2.

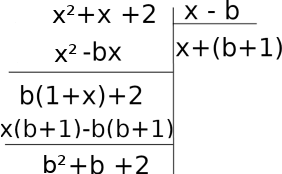
At each step we must remove the highest degree term: so in the 1st step we multiply x − b, by x to remove the x² and in the 2nd step to remove (b+1)x we multiply x − b, by b + 1. ■

«Polynomials: general properties Index gcd of polynomials »