Transformation Groups

A bijection X → X is often called a transformation on the set X, so a transformation group on X is a set of bijections on X which form a group under composition. Let X an arbitrary set. Consider the set 𝓢(X) of all transformations or bijections from X to itself: X → X. Under the operation of composition of functions (f ∘ g) (x) = f(g(x)), 𝓢(X) is a group since composition is associative, composition of bijections is a bijections, 1_X is a bijections, and every bijection has an inverse. I can be easily seen that 𝓢(X, ∘) is a non-Abelian group.

7.3.1 Definition A group G is said transformation group of a set X if G is a subgroup of the group 𝓢(X, ∘) of all bijections from X to itslef.  □

An example of transformation group is the group of planar isometries; Isometries are transformations that preserve distance. An isometry of ℝ² is a transformation φ: ℝ² → ℝ² that preserves distance, so that the distance between points P and Q is the same as the distance between the points φ(P) and φ(Q) for all points P and Q in ℝ². Note that if φ: ℝ² → ℝ² is a rigid motion, then φ sends the vertices of a triangle to the corresponding vertices of a congruent triangle. Hence, φ preserves the angles of a triangle.

If ψ is also an isometry of ℝ², then the distance between ψ(φ(P)) and ψ(φ(Q)) must be the same as the distance between φ(P) and φ(Q), which in turn is the distance between P and Q, showing that the composition of two isometries is again an isometry. Since the identity map is an isometry and the inverse of an isometry is an isometry, we see that the isometries of ℝ² form a subgroup of the group of all transformations of ℝ².

The isometries of the plane form a group under composition of function, the so called Euclidean group E₂. Euclidean group is built from the translational group T and the orthogonal group O₂(R).

Rotations and Reflections

Every element of O₂(R) can be represented by a 2 x 2 matrix, where any such matrix satisfies the condition A^TA = I. Let A be the matrix with respect to the standard basis for an element in O₂(R). If

then the condition A^TA = I gives

The relation above is satisfied for an angle θ with a = cos θ, c = cos θ, (b d) = (−sin θ, cos θ), or (b,d) = (sin θ, −cos θ). The first choice gives a matrix A with determinant 1 that represents a rotation

which are elements of the subgroup SO₂(R) of O₂. In particular, we have R_θR_φ = R_φR_θ, so the group SO₂ is Abelian.

On the other hand the second choice gives a matrix of determinant −1

that represents a reflection across a line through the origin. The elements of O2(R) \ SO₂(R) are reflections.

We can think of a reflection or a flip across a line l moves each point P to P ' such that line l is the perpendicular bisector of the segment connecting P and P′. If P is on l, then P is mapped to itself, or P = P'.

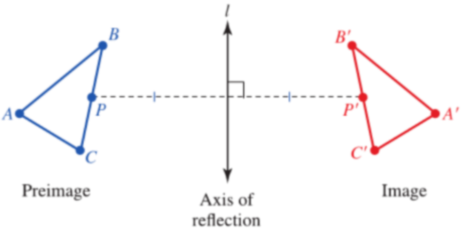
Reflections take the form

By applying two times such a transformation, the identity is obtained.

Rotations: Consider the following situation in which a point P of coordinates (x, y) is rotated about the origin of an angle θ to the point P' of coordinates (x', y').

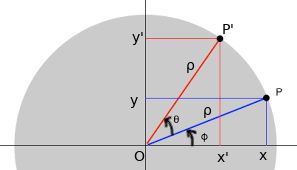
From the trigonometric relations

x = ρ cos φ,   y = ρ sin φ

and

x' = ρ cos (θ + φ) ,   y = ρ sin (θ + φ)

where ρ indicates the length of both OP and OP'. Since

ρ cos (θ + φ) = ρ cos θ ρ sin φ − ρ sin θ cos φ = x cos θ − y sin θ

ρ sin (θ + φ) = ρ sin θ ρ cos φ + ρ cos θ sin φ = x sin θ + y cos θ

we have

x' = x cos θ − y sin θ
y' = x sin θ + y sin θ

Introducing the column vector (x y) and (x' y') we can write the transformation as

$$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)$$

To reverse it, we apply the rotation −θ and obtain A⁻¹

$$A_{-\theta }=\left(\begin{array}{cc}cos\theta & sin\theta \\ -sin\theta & cos\theta \end{array}\right)$$

Translations

Let T denote the subgroup of E₂ which consists of all the translations. Translations slide every point the same distance in the same direction. Example: T(x, y) = (x, y) + (a, b) = (x + a, y + b), with a,b ∈ℝ² or equivalently

x' = x + a

y' = y + b

In vector form a translations by the vector v is the function τ: ℝ ⟶ ℝ² defined by τ(x) = v + x for all x ∈ ℝ². Translations— other than the trivial one, when v = 0 — cannot be linear because.

τ(x + y) = x + y + v ≠ τ(x) + τ(y) = x + y + 2v

Or, even more simply, we note that τ(0) = v, which must be 0 if τ is to be linear.

Since τ(0) = v, a translation is completely determined if we know where it sends the origin. This is easily checked τ(x) = 0 + x is the identity element. If τ₁, τ₂ ∈ T are defined by τ₁(x) = u + x and τ₂(x) = v + x for all x ∈ ℝ², then

τ₁τ₂⁻¹(x) = τ₁((−v) + x)
= u + ((−v) + x)
=(u − v) + x

So τ₁τ₂⁻¹ is translation by u − v and therefore belongs to T.

All these transformations can be represented by the following equations

x' = x cos θ + y sin θ + α.
y' = ε x sin θ −ε y cos θ + β.

with ε = ± 1. The matrix A = [cos θ, sin θ; ε x sin θ], is orthogonal with determinant ±1.