Inverse Function

Can the effect of a function be undone by an inverse function? We first define what an inverse function is

Definition 1.5.1. For a function f: X ⟶ Y an inverse function is a function g: Y ⟶ X such that f ∘ g and g ∘ f are the identity functions on Y and X respectively, that is

for all x in X and y in Y. Or

A function which has an inverse is said to be invertible.

Example 1.5.2 Consider the function f and g with domain and codomain ℝ which are defined by f(x) = 2x − 1 and g(x) = (x + 1)/2. The g is an inverse function of F since f ∘ g = id_ℝ. Indeed

with a similar comupation for g ∘ f. ■

A function f: X ⟶ Y need not have an inverse. For example, if f is not injective then there is a pre-image f⁻¹ for some y ∈ Y which contains at least two elements. In this case, it is not clear which of these two elements to choose for the value of the proospective inverse function with argument y. Likewise, if f is not surjective there exists an empty pre-image f⁻¹ so in this case there is no candidate for the value of a prospective inverse function at y.
A basic theorem asserts that only bijective functions are invertible.

Theorem 1.5.3. A function f: X ⟶ Y has an inverse if and only if it is bijective.

Proof. Suppose first that f has an inverse function g: Y ⟶ X. If f(x₁) = f(x₂), then, on applying g to both sides, we obtain g ∘ f(x₁) = g ∘ f(x₂). But g ∘ f is the identity function so x₁ = x₂. Hence f is injective. Next let y be any element of Y; then, since f ∘ g is the identity function, y = f ∘ g(y) = f(g(y)), which shows that y belongs to the image of f and f is surjective. Therefore f is bijective.
Conversely, assume that f is a bijective function. We need to find an inverse function g: Y ⟶ X for f. To this end let y ∈ Y; then, since F is surjective, y = f(x) for some x ∈ X; moreover x is uniquely determined by y since f is injective. This allows us to define g(y) to be x. Then g(f(x)) = g(y) = x and f(g(y)) = f(x) = y. Here it is necessary to observe that every element of X is of the form g(y) for some y in Y, so that g(f(x)) equals x for all elements x ∈ X. Therefore g is an inverse function for f.  □

The next observations is that when inverse functions do exists, they are unique.

Theorem 1.5.4. Every bijective function f: X ⟶ Y has a unique inverse function.

Proof. Suppose that f has two inverse functions, say g₁ and g₂. Then (g₁ ∘ f) ∘ g₂ = id_X ∘ g₂ = g₂ by Theorem 1.4.6 On the other hand, by Theorem 1.4.5 this function is also equatl to g₁ ∘ (f ∘ g₂) = g₁ ⋅ id_Y = g₁. Thus g₁ = g₂.  □

Note. Don't confuse f⁻¹(T) with the inverse function f⁻¹. The inverse function cannot be defined for any function, whereas the pre-image can always be defined.

Formally, this follows because both f and (f⁻¹)⁻¹ satisfy the condition in Def. 1.5.1.

Example 1.3.8. Let f: X → Y defined as in the example above, and let X₁ = {2,4} and B₁ = {B,C,E} then f(X₁) = {B, C} and f⁻¹(B₁) = {2,3,4}. ■

Example 1.3.9. Consider the function f: ℝ → ℝ defined as f(x) = x². Note that f({0,1,2}) = {0,1,4} and f⁻¹({0,1,4}) = {−2,−1,0,1,2}. This shows that f⁻¹(f(X)) ≠ X, since the function is not injective. ■

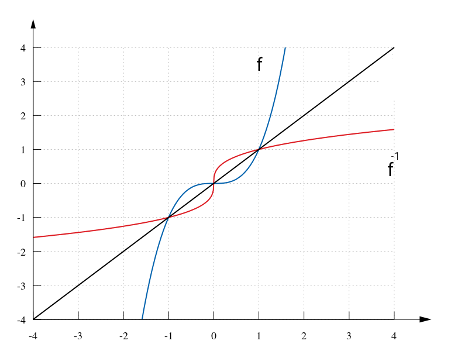
Graphic of the inverse function

Il grafico della funzione inversa si ottiene da quello di f scambiando tra loro le coordinate di ciascun punto (x₀, y₀). I punti (x₀, y₀) e (y₀, x₀), risultano simmetrici rispetto la retta y=x, bisettrice del I e III quadrante quindi i grafici di f e della sua inversa risultano uno l'immagine speculare dell'altro.

We want to represent the grap of f andf⁻¹ on the same cartesian plane. Since f(a) = b iff f⁻¹(b) = a, the point (a,b) belongs to the graph of f iff (b,a) belongs to the graph of f⁻¹. The point (b,a) is obtained from (a,b) by reflection about the line y = x

Some examples of function and inverse functions are the following

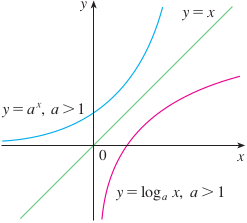
• The exponential function x ↦ a^x with its inverse, the logarithmic function x ↦ ln_a x.

  

• The trigonometric functions x ↦ sin x, x ↦ cos x and x ↦ tan x, with the inverses x ↦ arcsin x, x ↦ arccos x and x ↦ arctan x.

• The power function x ↦ xⁿ, for n ≥ 1, integer, with its inverse function: x ↦ x^1/n.

Un esempio è dato dalla funzione cubica: f(x) = x³ and f⁻¹(y) = (y)^1/3.