Fundamental Isomorphism Theorem for Groups
Theorem 7.13.1 (Kernel of a Homomorphism) For any homomorphism φ from the group G to the group G', Ker φ is a normal subgroup of G.
Proof. The identity e is in Ker φ since φ(e) = e', so Ker φ is always nonempty. If a ∈ Ker φ and b ∈ Ker φ, then φ(a) = e' and φ(b) = e'. Also, by Proposition 7.10.2, φ(b−1) = [φ(b)]−1, so.
φ(ab−1) = φ(a)φ(b−1)
= φ(a) [φ(b)]−1
= e' ⋅ (e')−1
= e'
and therefore ab−1 ∈ Ker φ. Thus, by Proposition 7.2.2., Ker φ is a subgroup of G. To show that Ker φ is normal, let x ∈ G and a ∈ Ker φ. Then
φ(xax−1) = φ(x)φ(a)φ(x−1) since φ is a homomorphism
= φ(x) ⋅ e' ⋅ φ(x) since a ∈ Ker φ
= φ(x) ⋅ φ(x−1) = e' by Proposition 7.10.2
Thus xax−1 is in Ker φ, and Ker φ is a normal subgroup by Propositions 7.11.7. □
We now state the Fundamental homomorphism theorem. We note that this is sometimes called the first group isomorphism theorem of group isomorphism theorem.
7.13.2 Fundamental homomorphism theorem for groups. Let G and G' two groups and let φ a homomorphism from the group G onto G'. Then there exists a unique isomorphism
φ*: G/Ker φ ≃ Im φ
such that
φ = φ* ∘ π
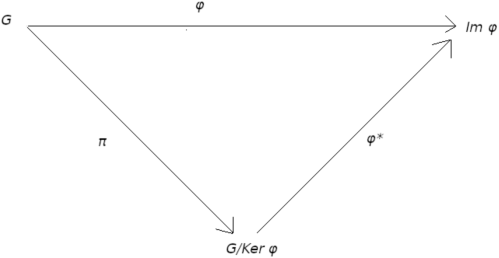
Proof. Let N = Ker φ. We define a mapping φ* from G/N onto Im φ as follows
φ*(Ng) := φ(g), ∀g ∈ G
We need to prove the following
The map φ* is well-defined i.e: Ng1 = Ng2 ⇒ φ(g1) = φ(g2).
φ* is bijective.
φ* is a group homomorphism.
Ng1 = Ng2 ⇐⇒ g1g2−1 ∈ Ker φ ⇐⇒ φ(g1g2−1) = e' ⇐⇒ φ(g1) = φ(g2)
We used proposition 7.8.2 on the equality of cosets to show that g1g2−1 ∈ Ker φ. Double implications prove at the same time that φ* is well-defined and injective.
For surjectivity notice that an element of Im φ, is of equal to φ(g) for some g ∈ G. But then φ(g) has as pre-image, through φ*, the coset Ker Ng, thus φ* is surjective.
φ*(Ker Ng1 * Ker Ng2) = φ*(Ker g1g2) = φ(g1g2) = φ(g1)φ(g2) = φ*(Ker Ng1) φ*(Ker Ng2) □
The first application of the previous theorem is the classification of cyclic groups.
7.12.3 Corollary. Let (G, ⋅), a cyclic group. Then,
(G, ·) is isomorphic to (ℤ, +) iff G is infinite;
(G, ·) is isomorphic to (ℤn, +) iff G is finite and |G| = n.
Proof. Let G = ⟨g⟩
φ: (ℤ, +) → G = ⟨g⟩
be the mapping defined by φ(k) = gk , where k ∈ ℤ. We have
φ(h + k) = gh+k = gh gk = φ(n)φ(k)
Suppose that G is infinite. In this case the integer powers are all distinct since if gh = gk, with k > h then gk − h = e so |g| is finite, a contradiction. Then h ≠ k implies that φ(k) = gk ≠ gk = φ(k), so the mapping φ is an injection and therefore it is an isomorphism, which implies Ker φ = {0}. For the fundamental group homomorpshim theorem G ≃ ℤ. This proves (i).
Suppose now G = ⟨g⟩ to have order n, then Ker φ = nℤ, from which
G ≃ ℤ/nℤ = ℤn □
7.12.4 Definition. An isomorphism of a group onto itself is called an automorphism.
Consider G abelian and the mapping φ:
φ: G ⟶ G
x ⟼ x−1
is an automorphism different from the identical automorphis if there exists in G an element x ≠ x−1. The condition to be abelian is required for φ to be a homomorphism that is φ(gh) = φ(g)φ(h); i.e. iff
(gh)−1 = (g−1)(h−1)
But (gh)−1 = h−1g−1 and so the condition is that g−1h−1 = h−1g−1 for all g,h ∈ G. Thus the condition is that G is Abelian (Any two inverses commute iff any two elements, commute, since as elements range over G so do inverses).
If φ(g) = φ(h) we have g−1 = h−1 and so g = h the mapping is thus 1-1.
We indicate with Aut(G) the set of all automorphism of the group G. It is easy to notice that (Aut(G), ∘) is a group, which is thus a subgroup of the group (S(G,∘) of all bijective mapping from G onto itself. Among the automorphism there is an important class known as inner automorphisms.
7.12.5 Definition. Let G a group. The mapping
Tg: G ⟶ G
x ⟼ gxg−1
is called an inner automorphism. □
The set 𝓘(G) = {Tg | g ∈ G} forms a normal subgroup of Aut(G). We seen already that the center of G is a normal subgroup of G. If the group G is abelian the center coincides with G and 𝓘(G) is reduced to the single indetinty automorphism. In general, 𝓘(G) is as smaller as larger the center of G is, how the following corolarry precises.
7.12.6 Corollary. Let G a group, 𝓘(G) the group of the automorphisms of G and Z(G) its center then we have that
𝓘(G) ≃ G/Z(G)
Proof. Consider the map,
φ: G → Aut(G)
g ⟼ Tg
The function, φ is a group homomorphism, and its kernel is precisely the center of G the image of φ is 𝓘(G). Then the result follows by the fundamental isomorphism theorem. □
7.12.7 Example. Let (ℝ \{0} , ·) be the multiplicative group of non-zero reals and GLn(ℝ) be the general linear group. Consider the map
φ: GLn(ℝ) → (ℝ \{0} , ·)
A ⟼ det A
φ is a surjective homomorphism, with kernel SLn(ℝ), hence GLn(ℝ)/SLn(ℝ) ≃ ℝ \{0}. ■
Lemma 7.12.8. Any automorphism of a cyclic group G (infinite or not) sends each single generator to some single generator.
Proof. Let G = ⟨g⟩ be a cyclic group then
ϕ(gn = e) = ϕ(g)n = e'. □
if |G| = n and G = ⟨g⟩ , then x = gi in G has G = ⟨gi⟩ iff (i,n) = 1
Example 7.12.9. The quotient group G/{e} ≅ G. The identity map φ:G → G: g ↦ g is surjective and injective, and its kernel is {e}, so by the fundamental homorphism theorem, G/ker φ = G/{e} ≅ G.