Euclidean algorithm

There is a useful algorithm for computing the GCD, of two integers a and b, (which we know to exists) called the Euclidean algorithm (also Euclid's algorithm). The Euclidean algorithm uses the division algorithm for integers repeatedly, and allow us to determine a Bézout identity as well. We want to calculate the gcd(a,b), we can without doubt let a ≥ b > 0.

2.4.1 Euclidean Algorithm. We write in bold the elements that are going to be divided in the next division. Let a, b ∈ ℤ and let a ≥ b > 0. We perform the following divisions:

We must come to an halt for sure (in less of b steps), since b >r₁ > r₂ > ... is a strictly decreasing sequence of positive integers.

Euclid's algorithm seems mysterious at first. The reason it works − the crux of the prood that the method yield gcd(a,b) − lies in the Lemma 2.2.5 that we rephrase as follows.

2.4.2 Lemma (Common gcd in stages of Euclid's Algorithm). If n = qd + r, then gcd (n,d) = gcd (d,r).

Proof. Suppose that n = qd + r. We shall prove that every common divisor of n and d is a common divisor of d and r and viceversa.
(⟶) Let c be a common divisor of n and d then c | (n − qd), i.e., c | r.
(⟵) Conversely, suppose c is a common divisor of d and r, then c | (qd + r), i.e. c | n. So c is a common divisor of d and n. Since their sets of common divisors are the same, gcd (n,d) = gcd (d,r).  □

Geometrical Representation of the Euclidean Algorithm

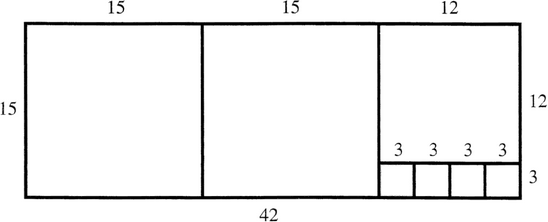
From a rectangle of side-lenghts a and b (a ≥ b) squares of side-lenght b are cut off, so long as it is possible. Then a remainder rectangle is left over, from which agains squares are cut off, and so on. The procedure continues, so long as the subdivision into squares is possible, that is, until no rectangle remains left over. The side-lenght of the smallest square is then the gcd of a and b. For the example a = 42, b = 15. Since the side-length of the smallest square is a common measure (indeed, the greatest common measure) of the original rectangle's side-lenghts a and b, the entire rectangle can be broken up into squares of this side-length.

The procedure for determining a possible unit common to two magnitudes, as line segments, angles, areas, can be regarded as the geometric equivalent of Euclid's algorithm. In the case of two line segments a, b, we consider the shortest one b and we cover a with copies of b. If we succeed in covering a perfectly, b is a common unit as a is a multiple of b. Otherwise, we consider the part c which remaind from a after covering it with copies of b, and restart the process uing c as the shortest segment between, this time, a and b. For the Pythagoreans this process would always stop after a finite number of steps, which is equivalent ot commensurability. However, the procedure will never stop in the case of the diagonal ad the side of a square.

The Pythagoreans of ancient Greece (500 B.C.) believed "all is number" and sought to explain the world in terms of ratios of whole numbers. They discovered that the ration of the diagonal to the side of a square is not a ratio of whole numbers, i.e. √2 is irrational: a real number which cannot be written as a quotient of two integers. If a and b are the lenghts of two line segments, a and b are commensurable if there are natural numbers k and h so that ka = hb: that is, placing k copies of the line segment of length a end-to-.end and h copies of the line segment of length b end-to-end give line segments of the same length. It was of interese to the Greeks to know when two line segments. The irrationality of the diagonal of the square of side 1 means that the side and the diagonal of a square are incommensurable. More generally, a line segment whose length is irrational is incommensurable with the line segment of unit lenght. For otherwise, there would be natural numbers, h, k so that k ⋅ a = h ⋅ 1, that is, a = h/k is rational.
The great Greek mathematician Eudoxus (ca. 360 B.C.) formulated a criterion for the commensurability of two constructible numbers a, and b, namely

Eudoxus's Criterion. The line segments a and b are commensurable, iff Euclid's algorithm applied to a and b stops.

Proof of the Euclid's algorithm

Note first that b > r₁ > r₂ > ··· > r_n > r_{n − 1} = 0 is a sequence of decreasing positive integers which cannot be continued indefinitely. Therefore the algorithm stops after no more than b divisions. From the divisions above we have that gcd(r_n, r_{n − 1}) = r_n and by applying the previous lemma repeatedly, we find that gcd(a,b) = gcd(r₁,b) = gcd(r₂,r₁) = ... = gcd(r_{n − 1}, r_{n − 2}) = gcd(r_n, r_{n − 1}) = r_n.  □

Example 2.4.3. Let a = 15 and b = 6.

15 = 6 ⋅ 2 + 3		gcd(15,6) = gcd (6,3)	By Lemma 2.4.2
6 = 3 ⋅ 2 + 0		gcd(6,3) = 3

Let's calculate gcd(34, 19) with the Euclidean algorithm.

34 = 19 ⋅ 1 + 15
19 = 15 ⋅ 1 + 4
15 = 4 ⋅ 3 + 3
4 = 3 ⋅ 1 + 1
3 = 1 ⋅3 + 0

Thus, gcd(34, 19) = 1.

Further, these relations offer us a way to write gcd(a,b) as Bézout's identity in the form d = gcd(a,b) = sa + tb. To find a Bézout's identity for per gcd(34, 19) = 1 = d, we proceed backward.

1 = 4 − 1 ⋅ 3
= 4 − 1(15 - 4⋅3) = 4 ⋅ 4 − 1⋅15
= 4(19 − 15⋅1) − 1⋅15) = 4⋅19 − 5⋅15
= 4⋅19 − 5(34 − 19⋅1) = 9⋅19 − 5⋅34

Thus Bézout's identity for a = 34 and b = 19 is 1 = 34(−5) + 19 ⋅ 9