The Integers

It is known that whilst the equation x − 3 = 0 ha a solutions in ℕ, the equation x + 3 = 0 has not. We want to extend the set ℕ in a way to include solutions to equations of the form x + n = 0, n ∈ ℕ. We are led in this way to the intger set ℤ = {...,-3,-2,-1,0,1,2,3...}. To introduce negative intergers we'll use notions already introduced in the previous chapters. We start from the cartesian product ℕ x ℕ, the set of all ordered pairs of natural numbers, with the following relation

an equivalence relation. Two ordered couples (n,m) and (n',m') of integers are euqal if n + m' = m + n'. The set ℕ x ℕ is partitioned in classes (n,m).

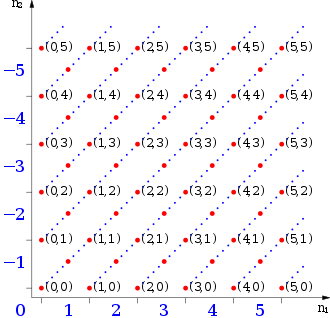
thus the couples (1,0), (2,1), (3,2) on the same diagonal are equivalence classes (1 + 2 = 3 + 0) and represent the same integer 1. As representetive of each class it is possible to choose particular couples, those in which one of the elements is zero. Geometrically, by those couple located on coordinate axis

The integers set defined as

ℤ can be decomposed in the following subsets:

where

The elements of ℤ⁺ are named positive integers, the one of ℤ⁻ negative integers.

The set ℤ is an extension of ℕ, because it contains a subset ℤ⁺ ∪ {0} that corresponds to ℕ through the injective map from ℕ to ℤ that maps to every natural integer n, the class (n,0)|. In the set ℤ is possible to define two operations: addition and multiplication in the following way:

Remarks

1. These are well-defined operations (see exercise 2): even though they are defined by representatives of classes, they do not depend on which representative is chosen.

2. From now on we'll indicate the elements of ℤ in the following way:

   (n,0) := n,   (0,0) := 0,   (0,n) := −n

3. ℤ with respect to the two operations of addition and multiplication just defined, has the following properties:

   1. a + b = b + a,   ∀a,b ∈ ℤ   (commutative property of addition)

   2. a ⋅ b = b ⋅ a,   ∀ a,b ∈ ℤ (commutative property of multiplication))

   3. (a + b) + c = a + (b + c),   ∀a,b,c ∈ ℤ   (addition is associative)

   4. (a ⋅ b) ⋅ c = a ⋅ (b ⋅ c), ∀a,b,c ∈ ℤ, (multiplication is associative)

   5. there exists a unique element 0 ∈ ℤ such that a + 0 = 0 + a, ∀a ∈ ℤ   (existence of the additive identity)

   6. ∀a ∈ ℤ there exists a unique element −a, such that a + (−a) = (−a) + a = 0   (existence of the inverse)

   7. there exists in ℤ a unique element, 1, such that a ⋅ 1 = 1 ⋅ a, ∀a ∈ ℤ (existence of the multiplicative identity)

   8. a ⋅ (b + c) = a ⋅ b + a ⋅ c, (a + b) ⋅ c = a ⋅ c + b ⋅ c, ∀a,b,c ∈ ℤ (Multiplication is distributive with respect to addition)

Lemma 2.1.1. Let a, b be elements of ℤ. Then

1. a ⋅ 0 = 0 ⋅ a = 0;

2. (−a) ⋅ b = −(a ⋅ b);

3. (−a) ⋅ (−b) = ab.

Proof

1. It results 0 + (a ⋅ 0) = a ⋅ 0 = a ⋅ (0 + 0) = a ⋅ 0 + a ⋅ 0, thus a ⋅ 0 = 0.

2. 0 = 0 ⋅ b = (a + (a)) ⋅ b = a ⋅ b + (−a) ⋅ b, thus (−a) ⋅ b = −(a ⋅ b).

3. (−a) ⋅ (−b) = per (ii) = −(a(−b)) = −(−(ab)) = ab.□

Proof. Note that if a and b are both positive or both negatives, their product is always postive or negative (if they are both positives, rembember the definition of product in ℕ, if they are both negatives consider the (iii) in the above proposition). If instead a > 0 and b < 0, then −b is positive, thus a(−b) = −ab is positive, and ab is negative. Thus if ab = 0 necessarily either a or b must be null. The inverse is obviuos from the lemma above property (i). □

Definition 2.1.3. The absolute value of an integer a is defined as the positive number:

Note that −b ≤ a ≤ b for a,b integers (or real) is equivalent to |a| ≤ b.

Let a,b ∈ ℤ, the following relations hold: