Complex Numbers
Over the set of ordered pairs of reals numbers
ℂ = ℝ x ℝ
we define the following two operations
(a,b) + (c,d) := (a + c, b + d)
(a,b) ⋅ (c,d) := (ac − bd, ad + bc)
This set is a field: the pair (0,0) is the neuter element for addition, (1,0) is the neuter element for multiplication. If (a,b) ≠ (0,0), then
(a,b) ⋅ (a/(a2 + b2), −b/(a2 + b2)) = (1,0)
Thus each element posses a multiplicative inverse as well.
The set of pairs (a,0), a ∈ ℝ, is the set of reals numbers, because the mapping
f: ℝ ⟶ ℂ
r ⟼ (r, 0)
is an injection, such that f(r + r') = f(r) + f(r') and f(r ⋅ r') = f(r) ⋅ f(r') ∀r,r' ∈ ℝ.
Definition 4.13.1 A complex number is an ordered pair of real numbers, i.e. an element of ℂ = ℝ x ℝ. With respect to the operations defined above, ℂ is a field, containing the real field.
If we indicate the pair (0,1) with the symbol i, we can write
(a,b) = (a,0) + (0,b) = (a, 0) + (0,1)(b,0) = a + ib
i2 = (0,1)(0,1) = −1
The element i ∈ ℂ is known as imaginary unit. Using this notation we have
(a + ib) + (c + id) = (a + c) + i (b + d)
To add two complex numbers together we just add up their real and imaginary parts.
(a + ib) ⋅ (c + id) = (ac − bd) + i (ad + bc)
We multiply two complex numbers together as we multiply real numbers together, and we make use of the fact that i2 = −1.
We can thus think of ℂ much like we think of ℝ2 (i.e., we think of the complex number a + bi ∈ ℂ as the vector (a, b) ∈ ℝ2), but with a multiplication operation that we do not have on ℝ2.
Given z = x + iy, we call complex conjugate of z and we denote it by z̄ the number
z̄ = x − iy
for example,
4 + 5i = 4 − 5i, 6 − 7i = 6 + 7i, 2i = −2i, 7̄ = 7.
Complex conjugates give us another way to interpret reciprocals. You can easily verify that a complex number z = x + yi times its conjugate x – yi is the square of its absolute value |z|2.
zz̄ = |z|2
Therefore, 1/z is the conjugate of z divided by the square of its absolute value |z|2.
1/z = z̄ / |z|2
Division of complex numbers
Consider 11 + 6i divided by 2 + 3i: 11 + 6i / 2 + 3i; this ratio can be written as a complex number in the form a + bi if we multiply numnerator and denominator by 2 − 3i
(11 + 6i) / (2 + 3i) = (11 + 6i) (2 − 3i)/(2 + 3i) (2 − 3i) = 40 − 21i / 13 = 40/13 − 21i/13
Given z, z1 and z2 the following identities hold
(z̄) = z
(z1 + z2) = z̄1 + z̄2
(z1z2) = z̄1z̄2
z = z̄ ⇐⇒ z ∈ ℝ
zz̄ = x2 + y2 is a real number ≥0; if z ≠ 0, zz̄ > 0
The real number zz̄ is known as norm of the complex number z and its square root is knwon as modulus of z and indicated by |z|.
Definition 4.13.2 For any complex number z1 = a + bi and z2 = c + di
|z1z2| = |z1| |z2|
Proof. Suppose z1 = a + bi and z2 = c + di are complex numbers. Then
|z1z2| = |(ac − bd) + (ad + bc)|2 = (ac − bd)2 + (ad + bc)2
=
a2c2 + b2d2 + a2d2 + b2c2 = (a2 + b2) (c2 + d2)
= |z1|2 |z2|2.□
The following properties hold
|z1 + z2| ≤ |z1| + |z2|
The last identity is known as Triangle Inequality. If we identify the complex number z = x + iy as the point of the plane P(x,y) the modulus |z| represents the lenght of the segment OP.
Geometrically, the right-hand part of the triangle inequality states that the sum of the lengths of any two sides of a triangle is greater than the length of the remaining side.
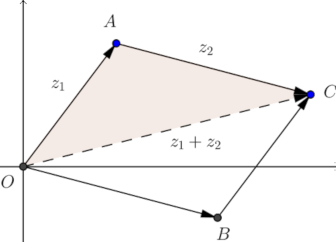
Complex plane; Trigonometric and polar forms of complex numbers
Much like we think of ℝ as a line, we can think of ℂ as a plane, called the complex plane. The set of real numbers takes the place of the x-axis (which we call the real axis) and the set of imaginary numbers takes the place of the y-axis (which we called the imaginary axis), so that the number a + bi has coordinates (a, b) on that plane, as in the following Figure

The number corresponds to the modulus or absolute value of x + yi and the angle θ is called the argument or amplitude of x + yi.
With the similarities with ℝ2 in mind, the absolute value is the norm or magnitude of a complex number a + bi, denoted as
which is simply the length of the associated vector (x, y) (i.e., it is the distance between x + yi and the origin in the complex plane).
Let θ be the angle subtended between the positive real axis and the line segment OP, and let r2 = x2 + y2, we have the following relations
x = r cos θ y = r sin θ
Thus we can represent the complex number x + iy in the following trigonometric form
x + iy = r(cos θ + i sin θ)
The angle θ is known as the argument of the complex number z, the number r corresponds to the modulus of z: r = |z| = (x2 + y2)1/2. The modulus, r, is unique, but the angle θ is not unique since there are many angles in standard position with P on their terminal side.
Euler's identity provides yet another convenient way to represent complex numbers. Indeed, if z = r(cos θ + i sin θ) is a complex number, then since eiθ = cos θ + i sin θ), we obtain the exponential representation or polar form
z = reiθ
When we multiply two complex numbers, geometrically what happens is that we multiply their distances to their origin and you add thei angles.
z1 ⋅ z2 = reiθ1 ⋅ r'eiθ2 = r1r2 ei(θ1 + θ2)
De Moivre’s formula
If z and z' have the following representation z = r[cosθ + i sinθ] and z' = r'(cosθ' + i sinθ') then as it can be easily verified
z ⋅ z' = rr' [cos (θ + θ') + i sin(θ + θ')]
the product of two complex numbers in trigonometric form is equal to a complex number having as argument the sum of the arguments and as modulus the product of moduli. The trigonometric form of a complex number is particularly useful to calculate the powers; for every integer n > 0, we have the following relation known as De Moivre Formula, valid for every integer n and every θ ∈ ℝ
ζn = rn (cos nθ + i sin nθ) (4.13.1)
it results also
[r(cos θ + i sin θ)]−1 = r−1 [cos (−θ) + i sin (−θ)]
n-th roots
Proposition 4.13.3. Let n a positive integer greater than 1, and let u and ζ two complex numbers. If
ζn = u (4.13.2)
there are precisely n complex roots of equation 4.13.2, and ζ is known as an nth root of u.
Proof. Let
u = r(cos θ + i sin θ), ζ = ρ(cos φ + i sin φ)
since ζn = u, we can deduce that r = ρn, i.e. ρ = r1/n, thus ρ is the unique real positive number such that the n-th power is r. Moreover from zn = u we can deduce as well that: cos nφ = cos θ and sin nφ = sin θ, then nφ = θ + 2kπ, i.e.
For an arbitrary integer k ∈ ℤ, we obtain the complex number
For k = 0, 1, n−1 the ζk are all distinct and represent the n-th roots of u. □
For u = 0 there is a unique root which is zero. For u = 1, we have the n-th roots of unity.
Definition 4.13.4 The roots in ℂ of the polynomial xn − 1 are called the complex nth roots of unity.
If ζ is an nth root of unity, and if n is the smallest positive integer for which ζn = 1, we say that ζ is a primitive nth root of unity. Thus, i is an 8th root of unity, but it is not a primitive 8th root of unity; however, i is a primitive 4th root of unity.
For u = 1, we have the nth roots of unity: 1 = cos(nθ) + i sin(nθ), and hence cos(nθ) = 1 and sin(nθ) = 0. The only way this can be verified is when nθ is an integer multiple of 2π, or equivalently θ = 2kπ/n for some integer k. So the nth roots of unity are cos(2kπ/n) + i sin(2kπ/n), for k = 0,...,n − 1. Let
ζn,1 = ζ = cos(2kπ/n) + i sin(2kπ/n), k = 0, ..., n − 1.
Then every n-th root of the unit is equal by De Moivre formula, to the k-th power of ζ, i.e.
ζn,k = ζk, k = 0, ..., n − 1.
All nth roots of a complex number u may be obtained by multiplying one of these values by all the nth roots of unity. Indeed let z0 be one of the values of the n-th root of the number u, i.e., z0n = u and let ζ be an arbitrary value of the n-th root of unity, that is ζn = 1. Then
(z0 ⋅ ζ)n = u
z0, z0ζ, z0ζ2, ..., z0ζn − 1 (4.13.3)
In the complex plane, the n-th roots of unity correspond to the n vertices of a regular n-sided polygon inscribed inside the unit circle. We view the vertices of the pentagon as the five 5th roots of unity, that is, the five roots of ζ5 − 1 = 0.
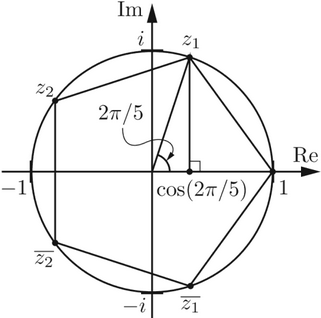
Example 4.13.5. Find the roots of x4 + 1.
Solution. We start by finding a particular solution: −1 = eiπ and taking the 4th root (−1)1/4 = ei π/4 = √2/2 + i √2/2. We know multiply this particular solution ω = √2/2 + i √2/2 = 1/√2 + i /√2, by the roots of unity. Notice that the primitive 4th root of unity” is just “i” or “−i”. We take i. Thus the four roots are
| 4th Roots of 1 | 1 | eiπ/2 | eπ | ei3π/2 |
|---|---|---|---|---|
| Four Roots of −1 | ω, | ωi, | ωi2, | ωi3 |
| ei π/4 ⋅ 1 = ω | ei π/4 ⋅ ei π/2 = ei 3π/4 | ei π/4 ⋅ ei π = ei 5π/4 | ei π/4 ⋅ ei 3π/2 = ei 7π/4 | |
| ω | ω3 | ω5 | ω7 | |
| 1/√2 + i /√2, | (1/√2 + i /√2)i, | (1/√2 + i /√2)i2 | (1/√2 + i /√2)i3 |
Thus the roots are (1 ± i)/√2 and (−1 ± i)/√2. ■
Proposition 4.13.3 states that the equation zn = a (with a complex) has exactly n complex solutions. However in the real field the equation xn +a can have one, two or no solutions (e.g. x2 − 1 = 0, x3 − 1 = 0, x2 + 1 = 0); Now we know that there are always n roots in ℂ, and eventually one or two of those roots are also in ℝ.
This result can be generalized to an arbitrary equation with degree n as follows:
Theorem 4.13.5. (Fundamental Theorem of algebra) A polynomial
a0 + a1z + ... + anzn = 0 (an ≠ 0)
with ai ∈ ℂ has exactly n roots in ℂ (counting multiplicity).
Exercises
Find the roots of x3 − 1.
Calculate the module of the following complex numbers
1 + i + i2 + i3 + i4 + i5
(1 + i)2
(1 + i)(1 − i)
Calculate
Write in algebraic form (1 + i)7.
Calculate
The 4-th roots of i.
The primitive 6th roots of the unity
Solutions
Let a primitive root
ω = cos(2π/3) + i sin(2π/3) 2
Then the roots are
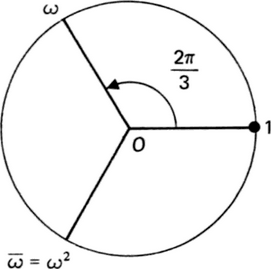
Both ω and ω are primitive cube roots of unity while 1 is obviously not. ■
-
|1 + i −1 + − i + 1 + i| = |1 + i| = √2
(1 + i)2 = (1 + 2i −1) = 2i, thus the module is (0 + 22)1/2 = 2.
|(1 + i)(1 − i)| = |1 −i + i + 1| = |2| = 2.
The modulus of (1 + i) is √2 and the argument π/4. Then in exponential form
√2 [cos (π/4 + 2kπ) + i sin (π/4 + 2kπ)] for k = 0,1,2,3,4
The 5th roots of unity are
(2)1/10 [cos (π/20 + 2kπ/5) + i sin (π/20 + 2kπ/5)] for k = 0,1,2,3,4
We calculate the modulus and argument and then apply De Moivre law
|1 + i| = √2 arg(1 + i) = π/4
Thus 1 + i = √2eiπ/4
(1 + i)7 = (√2eiπ/4)7 = (√2)7 ei 7π/4 = 8√2ei 7π/4
This can be rewritten as (1 + i)7 = (√2)7 ei 7π/4 = 8√2[ei8π/4 − π/4] = 8√2[e−π/4] = 8√2 [cos π/4 − i sin π/4] = 8√2 (1/√2 − i/√2) = 8 − 8i. ■
-
i = r (cos θ + i sin θ) con θ = π/2, r = 1. The four roots are zk = cos (θ + 2kπ/4) + i sin (θ + 2kπ/4), with k = 0,1,2,3. Replacing θ = π/2: zk = cos (π/2 + kπ/2) + i sin (π/2 + kπ/2), with k = 0,1,2,3
zk = cos (2kπ/6) + i sin (2kπ/6), with k = 0,1,2,3,4,5. The primitive roots are those satisfying zk ≠ 1, namely those for k = 1, k = 5.